Закон количества движения

Одной из важнейших задач гидромеханики является определение силового суммарного воздействия со стороны жидкости на тело. Для определения гидродинамических реакций можно воспользоваться законом количества движения и законом моментов количества движения, применение которых при установившемся течении жидкости особенно эффективно. Эти законы в применении к жидкости приобретают специфическую форму.

Начнем с рассмотрения закона количества движения. Его формулировка известна из механики: производная по времени от вектора количества движения материальной системы (жидкости) равна главному вектору всех внешних сил , приложенных к системе

, (3.15)

где в случае жидкости — главный вектор массовых сил, а — главный вектор поверхностных сил, приложенных на ограничивающих ее объем поверхностях.

Выделим в жидкости произвольный жидкий объем V, ограниченный в начальный момент времени неподвижной в пространстве поверхностью S (рис.14).

Внутри жидкого тела может находиться твердое тело (или тела), ограниченное поверхностью S _т. Ориентируем нормали к этим поверхностям вовне по отношению к объему жидкости. Выделим частицу жидкости с массой rdV. Если скорость этой частицы , то элементарный вектор ее количества движения определится равенством . Вектор количества движения жидкого объема V найдется интегрированием по всему объему

. (3.16)

В общем случае для вычисления необходимо знать поле скоростей во всем объеме V. Покажем, что при установившемся течении жидкости достаточно знать только скорость на границе объема, т.е. на контрольной поверхности S + S _т.

Для доказательства этого вычислим изменение количества движения. За промежуток времени выделенный жидкий объем протечет через контрольную поверхность и займет положение, ограниченное поверхностью S’. Поверхности S’ и S будем считать бесконечно близкими.

При установившемся движении жидкости, когда скорости не зависят от времени, количество движения жидкости в области пространства, общей для поверхностей S’ и S, в разные моменты времени одно и то же, т.е. в ней . Следовательно, изменение количества движения объема жидкости V связано только с перетеканием части ее через контрольную поверхность. Количество движения вышедшего и вошедшего объемов легко подсчитать. Для этого выделим на контрольной поверхности элементарную площадку , вектор скорости в центре площадки обозначим , нормальную составляющую скорости . За время через эту площадку протечет количество жидкости , масса протекающей жидкости определится выражением , а вектор элементарного количества движения будет . Общее изменение количества движения за счет протекания жидкости через контрольную поверхность S получается интегрированием по этой поверхности элементарных количеств движения . В этом выражении вынесено за знак интеграла, так как контрольная поверхность неподвижна в пространстве. Искомое выражение для производной количества движения при установившемся течении жидкости приобретает вид

, (3.17)

т.е. производная количества движения при установившемся течении равна потоку количества движения сквозь контрольную поверхность.

Получим выражения для главных векторов массовых и поверхностных сил. Если 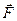- напряжение массовых сил, то главный вектор массовых сил . Главный вектор поверхностных сил может быть выражен через напряжения поверхностных сил 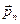: . Подставляя полученные выше выражения в (3.15), перепишем (3.15) в следующей форме:

, (3.18)

представляющей общее выражение закона количества движения при установившемся течении жидкости. Поскольку при выводе этого закона не делалось никаких предположений о роде жидкости, он одинаково справедлив для вязкой и невязкой жидкости.

Весьма важным является случай, когда можно пренебречь массовыми силами. Здесь лишь напомним, что при этом под напряжением необходимо понимать избыточные гидродинамические величины за вычетом гидростатического давления. Массовые силы тяжести, действующие на жидкость, в этом случае приводят к появлению на теле S силы Архимеда, которую всегда можно учесть отдельно. В этом случае выражение закона количества движения приобретает следующий вид:

. (3.19)

При обтекании твердого тела, ограниченного поверхностью S _т, на нем соблюдается условие непротекания . Интеграл представляет гидродинамическую реакцию воздействия тела на жидкость. Согласно третьему закону Ньютона реакция жидкости на тело равна . Исходя из этого, можно из (3.19) получить следующую формулу для определения гидродинамической реакции:

. (3.20)

Основная ценность закона количества движения, представленного в этих формах, заключается в том, что в обеих частях этих выражений содержатся только интегралы по контрольной поверхности S. Иными словами, для применения этого закона нужно знать картину движения жидкости не во всем объеме, а только на его контрольной поверхности, которая может быть выбрана произвольно, исходя из соображений удобства вычислений и знания величин скоростей и напряжений на отдельных ее участках.

Для невязкой жидкости и закон количества движения представится в виде

(3.21)

или в проекциях на оси координат

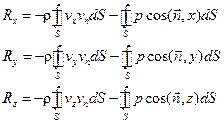(3.22)

Аналогично может быть получен закон моментов количества движения. Если — радиус-вектор центра площадки на контрольной поверхности, то момент количества движения элементарного вышедшего объема получается векторным умножением на его количество движения. Таким образом, при установившемся течении закон моментов количества движения примет вид

, (3.23)

где правая часть выражает момент поверхностных сил.

Поиск по сайту: