Обтекание кругового цилиндра с циркуляцией

Наложим на обтекание кругового цилиндра плоский вихрь (циркуляционный поток) с центром в начале координат (1.1.14).

Потенциал суммарного течения будет иметь вид

, (1.3.1)

а функция тока

. (1.3.2)

Получим выражения для скоростей этого потока

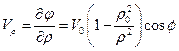, (1.3.3)

. (1.3.4)

Из формулы (1.3.3) видно, что добавление плоского вихря не влияет на величину радиальной скорости, и, соответственно, не нарушает условие непротекания на поверхности цилиндра, где выражения для скоростей принимают вид

. (1.3.5)

Найдем положение критических точек на поверхности цилиндра. В критических точках скорость равна нулю, откуда получим

;

(1.3.6)

В зависимости от величины циркуляции G возможны четыре варианта решения уравнения (1.3.6):

1) ; ;

, ,

получаем бесциркуляционное обтекание цилиндра (п.1.2, рис.5);

2) ; ;

например, при получаем ;

, - такое течение изображено на рис.6;

Рис. 5

3) ; ;

- течение с одной критической точкой (рис.7);

Рис. 6

4) ;

решения не существует, следовательно, на поверхности цилиндра нет критических точек. Такое течение изображено на рис.8, где видно, что критическая точка расположена выше цилиндра, а часть примыкающей к цилиндру жидкости вовлечена во вращательное движение.

Рис. 7

Рассмотрим случай 2) более подробно. При этом варианте течения скорость на верхней части цилиндра при

, (1.3.7)

а по нижней стороне цилиндра при

, (1.3.8)

то есть в симметричных точках . Коэффициент давления на верхней и нижней сторонах цилиндра также будет разным

, (1.3.9)

, (1.3.10)

причем в соответствующих точках () , что при интегрировании давлений по поверхности цилиндра даст гидродинамическую силу .

Получим выражение для R_y. Рассмотрим элемент площади поверхности цилиндра

.

К этой площади приложено избыточное давление

.

Элементарная сила избыточного давления, действующая на площадь dS, выражается в виде

,

причем на окружности , а знак «минус» появляется, так как сила направлена внутрь цилиндра, а нормаль – наоборот.

Элементарная вертикальная сила записывается в виде

.

Проинтегрируем dR_y по поверхности цилиндра

,

где r - плотность жидкости, а коэффициент давления имеет вид

Подставим это выражение в формулу для R_y:

После необходимых вычислений получим выражение для подъемной силы при обтекании цилиндра с циркуляцией

. (1.3.11)

Направление силы перпендикулярно скорости набегающего потока. Для того, чтобы определить это направление, необходимо повернуть вектор скорости набегающего потока на 90⁰ против направления циркуляции. При этом необходимо учитывать, что при вращении жидкости против часовой стрелки циркуляция принимается положительной.

Поиск по сайту: