Основы теории подобия в гидромеханике. Геометрическое и кинематическое подобие

В большинстве случаев система дифференциальных уравнений движения вязкой жидкости (4.7) не может быть проинтегрирована. Поэтому многие практические задачи решаются с помощью экспериментальной гидромеханики. Такие важные задачи, как определение сопротивления судна, необходимое для выбора мощности главных механизмов, подбор гребных винтов и пр., до сих пор не могут быть решены с достаточной строгостью без проведения экспериментов.

Возможны два типа экспериментов: с натурными объектами и с моделями. Наиболее ценными являются натурные опыты, дающие непосредственный ответ на вопрос, как ведет себя натурный объект в заданных условиях движения в жидкости, но они, как правило, дороги, технически очень сложны, сильно зависят от метеорологических условий, а в ряде случаев технически просто невыполнимы.

В силу этих причин в гидромеханике прибегают к постановке модельных экспериментов, осуществляемых на объектах, размеры которых иногда во много раз меньше натурных. При этом важно уметь правильно поставить опыт, чтобы его результаты можно было пересчитать на натурный объект, для чего нужно знать, в каком соотношении находятся скорости и силы, действующие на модель и натуру. Все эти вопросы рассматриваются в разделе гидромеханики, носящем название теории подобия и моделирования.

Опытные материалы для удобства сопоставления и работы с ними представляются, как правило, в безразмерном виде. Выбор безразмерных параметров, от которых зависит явление, также осуществляется с помощью теории подобия.

Для соблюдения механического подобия двух течений, происходящих вокруг натурного объекта и его модели, требуется одновременное выполнение трех условий подобия: 1) геометрического; 2) кинематического (по скоростям); и 3) динамического (по силам). Первые два условия являются необходимыми, но недостаточными. Динамическое подобие обеспечивает достаточность условий подобия явлений.

Сформулируем математически требования, вытекающие из условий геометрического и кинематического подобия. Все элементы, относящиеся к модели, будем обозначать индексом «м», а к натурному – индексом «н».

Отметим, что натура и модель могут двигаться (обтекаться) различными жидкостями с разными плотностями и и коэффициентами кинематической вязкости и (например, вода, воздух).

Условия геометрического подобия заключаются в том, что сходственные геометрически размеры в потоках на модели и натуре должны быть пропорциональны. Если через обозначить какие–либо сходственные размеры в потоках (например, ширину канала, координаты сходственных точек), через и - характерные линейные сходственные размеры (например, длину тела), то для соблюдения геометрического подобия потребуется, чтобы

. (4.8)

Постоянная величина k_L называется модулем геометрического подобия. Эта величина обратна масштабу модели. Как правило, k_L >>1. Из (4.8) следует, что все сходственные размеры натуры получаются умножением размеров модели на модуль геометрического подобия. Отношение сходственных площадей S и объемов W в двух геометрически подобных потоках будет соответственно

; . (4.9)

Из (4.8) следует, что . Величина является безразмерной координатой. На этом основании можно заключить, что безразмерные координаты сходственных точек модели и натуры равны

. (4.10)

Кинематическое условие подобия заключается в том, что скорости в сходственных точках потока объекта и его модели в сходственные моменты времени должны быть пропорциональны. Обозначим через , соответственно проекции скоростей в сходственных точках модели и натуры, через , их характерные скорости (например, скорость движения тела), а через 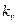– масштаб скоростей. Тогда аналогично (4.8) условие кинематического подобия будет

. (4.11)

Его можно переписать в виде

или , (4.12)

где введены безразмерные проекции скоростей .

Поскольку в сходственных точках потоков безразмерные скорости равны, то должны быть одинаковы и эпюры безразмерных скоростей в потоках модели и натуры.

Если движение жидкости неустановившееся, то сравнивать скорости имеет смысл только в сходственные моменты времени. Обозначим через и промежутки времени для натуры и модели, через и – характерные промежутки времени (например, период колебаний для процессов колебательного характера или время, в течение которого тело проходит путь, равный его длине) и введем безразмерные промежутки времени

. (4.13)

В сходственные моменты времени безразмерное время одинаково

. (4.14)

Поиск по сайту: