Условия динамического подобия

Перейдем теперь к формулировке условий динамического подобия, связывающего силы различной природы, действующие в потоках модели и натуры. Используем метод получения условий динамического подобия, основанный на анализе уравнений движения жидкости.

Запишем уравнение движения вязкой жидкости в проекции на ось z:

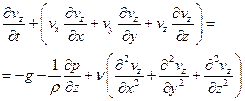(4.15)

Введем в рассмотрение характерные постоянные величины: линейный размер L, скорость v₀, характерное время T и характерное давление P.

Для координат, проекций скоростей, времени t и давления p можно записать

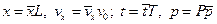. (4.16)

Преобразуем уравнение (4.15), введя в него безразмерные и характерные величины. Поскольку характерные величины являются постоянными, их можно выносить из-под знака дифференциала. При этом получим

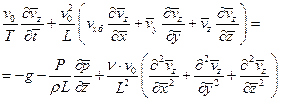. (4.17)

В этом уравнении все производные – безразмерные величины. Из структуры данного уравнения следует, что член 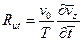представляет удельную (отнесенную к массе) силу инерции нестационарной природы; - сила инерции конвективной природы; 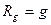– сила тяжести; 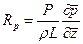- сила давления; 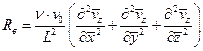- сила вязкости. Для соблюдения динамического подобия аналогично предыдущим соображениям потребуем, чтобы силы различных категорий, действующих на натуру и модель, были бы пропорциональны

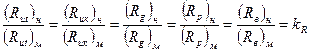, (4.18)

где 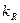– модуль динамического подобия.

Выберем в качестве характерной силы, которая имеет место во всех случаях движения, силу инерции конвективной природы 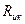. Используя основное свойство пропорций, запишем:

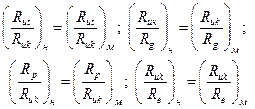. (4.19)

Система этих четырех равенств эквивалентна записанному выше условию динамического подобия. Подчеркнем, что для выполнения подобия, эти равенства должны выполняться совместно (одновременно). Рассмотрим последовательно эти равенства, начав с четвертого из них:

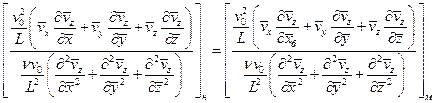(4.20)

Согласно полученным выше условиям геометрического и кинематического подобия , , 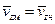откуда следует, что и безразмерные производные, входящие в записанные выше выражения, для модели и натуры также равны. С учетом этого получим, что для выполнения этого условия подобия по силам вязкости должно быть

. (4.21)

Этот безразмерный критерий динамического подобия, представляющий отношение сил инерции к силам вязкости, носит название критерия (числа) Рейнольдса

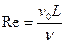. (4.22)

Таким образом, для выполнения подобия по силам вязкости, должно соблюдаться равенство по числам Рейнольдса

.

Отношение сил инерции к силам тяжести 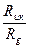выразится как 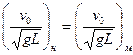. В судовой гидромеханике вместо этой величины используют комплекс

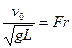, (4.23)

называемый числом Фруда. Таким образом, должно быть

.

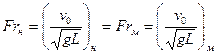Отношение сил давления к силам инерции (третий член в (4.19)) представится в виде:

,

Безразмерный комплекс

(4.24)

называется критерием подобия Эйлера. Таким образом, должно быть

. (4.25)

Соблюдение равенства (4.25) необходимо при моделировании процессов, обусловленных силами давления. Однако, можно показать, что в случае отсутствия кавитации – процесса, зависящего от давления, число Эйлера не является определяющим, т.е. при выполнении подобия по числам Фруда и Рейнольдса подобие по числам Эйлера выполняется автоматически. В случае же кавитационных процессов, число Эйлера является определяющим и представляется в виде так называемого числа кавитации

(4.26)

Наконец, отношение сил инерции нестационарной природы к конвективным силам инерции представится в виде

.

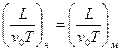Этот безразмерный комплекс носит название критерия подобия (числа) Струхаля

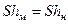; . (4.27)

Еще раз подчеркнем, что для выполнения условий полного механического подобия необходимо соблюсти одновременное равенство всех четырех критериев подобия.

С учетом введенных критериев подобия, безразмерное уравнение движения жидкости запишется в виде

. (4.28)

Если в жидкости помимо перечисленных выше сил действуют силы других категорий, то для их учета при моделировании требуется введение дополнительных критериев подобия. В случаях, когда имеет место распространение струй, брызгообразование, распространение капиллярных волн, образование в жидкости каверн, существенное значение приобретают силы поверхностного натяжения. Для учета подобия по силам поверхностного натяжения вводится число Вебера

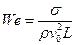, (4.29)

где s - коэффициент поверхностного натяжения жидкости.

Для подобия потоков с учетом сил поверхностного натяжения требуется соблюдение равенств чисел Вебера .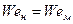

При движении сжимаемой жидкости (газа) с большими скоростями в число критериев подобия входит число Маха M, под которым понимают отношение характерной скорости к скорости звука a

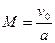. (4.30)

где a - скорость звука. Число Маха играет большую роль в газовой динамике. Для течений газа, близких к скорости звука и превосходящих ее, необходимо учитывать подобие по числам Маха. При M <1 течения газа называются дозвуковыми; качественно они аналогичны течениям несжимаемой жидкости.

Поиск по сайту: