Общие формулы для сил и моментов

Вернемся к уравнению движения вязкой жидкости в виде (4.17).

В этом уравнении все производные – безразмерные величины. Из структуры данного уравнения следует, что все слагаемые представляют удельные (отнесенные к массе) силы (нестационарной природы, инерции, массовые, силы давления, силы вязкостной природы). Умножим это уравнение на массу жидкости в виде 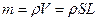и выделим в размерных множителях критерии подобия, после чего получим уравнение, связывающее размерные силы различной природы:

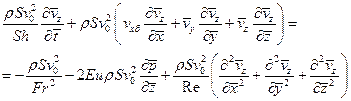(4.30)

Отношение сил одинаковой природы для натурного объекта R_н и для модели R_м получатся с учетом (4.18) в виде

.

Разделив уравнение (4.30) для натуры на такое же уравнение для модели, мы получим величину k_R: при выполнении условий динамического подобия

.

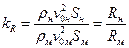То есть безразмерные силовые характеристики, полученные в виде , для модели и натуры будут одинаковыми

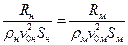. (4.31)

Безразмерные силовые характеристики в виде (4.31) называются безразмерными силовыми коэффициентами и обозначаются

. (4.32)

Аналогично вводятся безразмерные коэффициенты гидродинамических моментов, куда вводится характерное дополнительное плечо L

. (4.33)

Учитывая это, можно выражения для гидродинамической реакции и момента представить в виде

, (4.34)

Характерные величины v₀, S и L для каждого класса задач выбирают по-разному. Например, в случае движения судна обычно в качестве характерной длины выбирают длину по ватерлинии, а в качестве характерной скорости – скорость движения судна. За характерную площадь принимают смоченную поверхность, а иногда площадь миделевого сечения тела. При решении задач динамики тел в ряде случаев в качестве характерной площади целесообразно принимать , т.е. объемное водоизмещение тела в степени 2/3. Удачный выбор характерных величин способствует систематизации опытных материалов.

Итак, при выполнении условий полного динамического подобия для натурного объекта и геометрически подобной ему модели, коэффициенты гидродинамических сил равны, то есть

, (4.35)

откуда следует основной закон подобия: коэффициенты гидродинамических сил и моментов для модели и натуры равны, если соблюдается равенство всех критериев подобия.

При этом коэффициенты гидродинамической силы и момента являются функциями критериев подобия:

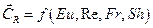, (4.36)

На практике обычно оперируют не векторным коэффициентом гидродинамической силы , а его составляющими по осям координат в поточной системе координат. Ось x направлена при этом по вектору скорости набегающего потока , где , , – соответственно коэффициенты сопротивления, подъемной и боковой силы (силы дрейфа).

При этом .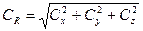

Для составляющих гидродинамической реакции аналогично получим выражения

. (4.37)

Поиск по сайту: