Сопротивление тела при установившемся движении

В общем случае суммарную гидродинамическую силу , действующую на тело, можно разложить на три составляющие, как показано на рис.16. Ось x здесь совпадает с направлением движения, ось y направлена вверх, а ось z - вбок.

Проекция суммарной гидродинамической силы на направление движения – R_x – называется силой сопротивления, R_y – подъемной силой и R_z – боковой силой или силой дрейфа.

Рассмотрим силу сопротивления жидкости при движении тела с постоянной скоростью.

На рис.17 показано обтекание осесимметричного тела потоком жидкости, что, согласно принципу обращения движения, в динамическом смысле, эквивалентно поступательному движению тела в жидкости с постоянной скоростью v₀. Для простоты рассуждения рассмотрим тело, симметричное относительно миделя. При обтекании такого тела невязкой жидкостью эпюра распределения коэффициента давления на теле будет также симметрична относительно миделя (см. рис.17). Следовательно, силы давления, действующие на носовую и кормовую части тела в проекции на направление движения (ось x), взаимно компенсируются, и результирующая сил давления будет равна нулю. Поскольку сопротивление трения в данном случае также отсутствует, то и полное сопротивление R_x равно нулю.

Это положение известно в гидромеханике как парадокс Эйлера-Д’Аламбера, который в общем виде формулируется следующим образом: при движении тела в невязкой безграничной жидкости с постоянной скоростью сила, действующая на тело со стороны жидкости, равна нулю.

Данный парадокс справедлив не только для симметричных тел, но и для тел любой произвольной формы и распространяется как на величину полной гидродинамической силы , так и на все ее проекции.

В реальной жидкости вследствие вязкости возникает прежде всего сопротивление трения R_{x тр}, которое является проекцией на направление движения результирующей силы касательных напряжений .

Кроме того, вязкость вызывает на теле перераспределение давлений по сравнению с давлениями в невязкой жидкости. На рис.17 показано пунктирной линией распределение давлений с учетом влияния вязкости. Из рисунка видно, что при движении тела в вязкой жидкости давление в корме ниже, чем в носу. Это обстоятельство обуславливает появление второй составляющей сопротивления – так называемого сопротивления формы R_{x ф}. Таким образом, сопротивление формы – это проекция на направление движения равнодействующей сил давления , приложенных к телу в безграничной жидкости.

При движении тела вблизи или по свободной поверхности жидкости на ней возникают волны, вызванные телом. В результате возникновения волн происходит дополнительное перераспределение давления по телу (по сравнению с его движением в безграничной жидкости), которое приводит в среднем к повышению давлений в носу и понижению в корме. В результате возникает так называемое волновое сопротивление R_{x волн} – проекция на направление движения равнодействующей дополнительных сил давления, вызванных деформацией свободной поверхности из-за волнообразования. При увеличении заглубления тела волновое сопротивление падает и при глубине h, превосходящей длину тела, становится практически равным нулю.

Энергетически волновое сопротивление тела можно представить себе как силу, работа которой расходуется на поддержание системы волн на свободной поверхности. Следует отметить, что волновое сопротивление, так же как и волны, обязано своим существованием силе тяжести, заставляющим жидкость колебаться после выведения ее из равновесия телом и образовывать систему волн. Значит, волновое сопротивление может существовать и в невязкой жидкости.

В результате для общего случая движения тела сила сопротивления равна

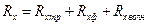(5.1)

Два первых слагаемых этого выражения часто объединяют в одно, называемое вязкостным сопротивлением:

,

тогда

.

В гидромеханике и теории корабля принимается предположение, что составляющие сопротивления не оказывают взаимного влияния друг на друга и что на R_{x тр} и R_{x ф} (вязкостные составляющие) не влияет сила тяжести, а на волновое сопротивление не влияет вязкость жидкости, т.е. последнюю составляющую можно рассчитывать с помощью аппарата динамики невязкой жидкости. В основе расчета R_{x тр} и R_{x ф} лежат методы теории пограничного слоя.

Если выражение (5.1) разделить почленно на 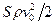, то в соответствии с (4.32) можно получить коэффициент сопротивления тела

,

где C_{x тр} – коэффициент сопротивления трения, C_{x ф} – коэффициент сопротивления формы, C_{x волн} – коэффициент волнового сопротивления.

В соответствии с физической природой составляющих сопротивления эти коэффициенты являются функциями различных критериев подобия:

, , .

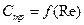Величины всех составляющих сопротивления также зависят от формы тела.

Поиск по сайту: