АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пространственный источник (сток)

Читайте также:
  1. I СИСТЕМА, ИСТОЧНИКИ, ИСТОРИЧЕСКАЯ ТРАДИЦИЯ РИМСКОГО ПРАВА
  2. I.4. Источники римского права
  3. II. Проблема источника и метода познания.
  4. Авторитаризм — источник отклоняющегося поведения
  5. Акмеизм как литературная школа. Основные этапы. Эстетика, философские источники. Манифесты.
  6. Анализ имущества организации и источников его финансирования.
  7. Анализ источников финансирования инвестиционных проектов
  8. Анализ наличия, состава и динамики источников формирования капитала предприятия
  9. Анализ равновесия между активами предприятия и источниками их формирования. Оценка финансовой устойчивости предприятия
  10. Анализ состава, структуры, источников формирования капитала организации и эффективности его использования.
  11. Антропогенное воздействие на атмосферу. Источники и последствия загрязнений.
  12. Антропогенное воздействие на гидросферу. Источники и последствия загрязнений.

Кроме плоских источника и стока в гидромеханике рассматриваются также пространственные источник и сток. Под таким течением подразумевается равномерное истечение жидкости во все стороны из точки – пространственный источник, или, соответственно, равномерное подтекание жидкости к точке – пространственный сток.

Найдем расход жидкости Q через сферическую поверхность радиуса r, центром которой является пространственный источник, расположенный в начале координат

,

при этом для данного пространственного источника расход жидкости характеризует его интенсивность и, по закону сохранения расхода, Q является одинаковым для сферической поверхности любого радиуса вокруг источника. Исходя из этого, можно выразить скорость течения жидкости от пространственного источника в любой точке пространства в виде

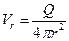(2.9)

Пользуясь формулами (2.3), и проведя преобразования, аналогичные тем, что сделаны для плоского источника, можно получить потенциал пространственного источника

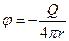, (2.10,а)

а также и для пространственного стока

. (2.10,б)

Для пространственного источника (стока) в произвольной точке (x1, y1, z1) потенциал примет вид

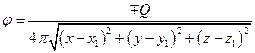. (2.11)

Необходимо отметить, что из формул (2.6) и (2.9) следует, что при r®0, то есть в самом источнике (стоке) скорость становится равной бесконечности. Точки, скорость в которых скорость теоретически становится равной бесконечности, называются особыми точками. В действительности физически скорость не может стать бесконечно большой. В связи с этим при сложении потенциальных потоков, в числе которых находится источник или сток, область, располагающаяся в непосредственной близости к источнику или стоку исключается из рассмотрения.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)