 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кинетическая энергия жидкости. Обобщенные присоединенные массы
Получим выражение для кинетической энергии безграничной жидкости в общем случае движения в ней твердого тела, ограниченного поверхностью S. Свяжем с телом систему координат 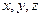 с центром в полюсе O, считая, что в данный момент времени она совпадает с неподвижной в пространстве системой координат
с центром в полюсе O, считая, что в данный момент времени она совпадает с неподвижной в пространстве системой координат  ,
, 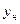 ,
,  . Проведем сферическую поверхность å большого радиуса
. Проведем сферическую поверхность å большого радиуса  с центром в начале координат.
с центром в начале координат.
Устремляя в дальнейшем радиус сферы к бесконечности  , получим случай безграничной жидкости. Обозначим вызванную скорость жидкости в произвольной точке между поверхностями S и å через
, получим случай безграничной жидкости. Обозначим вызванную скорость жидкости в произвольной точке между поверхностями S и å через  . На бесконечности жидкость покоится, т.е.
. На бесконечности жидкость покоится, т.е. 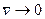 . Кинетическая энергия объема W¥, заключенного между поверхностями S+å, будет
. Кинетическая энергия объема W¥, заключенного между поверхностями S+å, будет
 . Вычисление этого выражения в общем случае затруднительно, так как для этого требуется знание скоростей во всем объеме вне тела.
. Вычисление этого выражения в общем случае затруднительно, так как для этого требуется знание скоростей во всем объеме вне тела.
Предположим, что вызванное движение жидкости безвихревое с однозначным потенциалом скорости j. Тогда  представится в виде
представится в виде 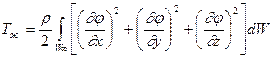 . Произведем тождественное преобразование членов, входящих в подынтегральное выражение:
. Произведем тождественное преобразование членов, входящих в подынтегральное выражение:

Сложив почленно правые и левые части этих выражений, получим

Поскольку потенциал скорости удовлетворяет уравнению Лапласа, последний член правой части данного равенства обращается в нуль, и выражение для кинетической энергии жидкости приобретает вид

 .
.
Применим формулу Гаусса - Остроградского, переводящую объемный интеграл в поверхностный (рис.19), обозначив при этом  - внешнюю нормаль к поверхностям S+å
- внешнюю нормаль к поверхностям S+å
 (5.8)
(5.8)
где 
Чтобы оценить интеграл по поверхности å сферы большого радиуса  , представим потенциал вызванных скоростей j вдали от тела в виде ряда по степеням
, представим потенциал вызванных скоростей j вдали от тела в виде ряда по степеням  . Единственно возможной формой представления j, удовлетворяющей этому граничному условию затухания движения на бесконечности, будет ряд следующего вида
. Единственно возможной формой представления j, удовлетворяющей этому граничному условию затухания движения на бесконечности, будет ряд следующего вида
 , (5.9)
, (5.9)
где A1 и An - коэффициенты, не зависящие от  . Вычислим
. Вычислим  на поверхности сферы å, учитывая, что направления нормали
на поверхности сферы å, учитывая, что направления нормали 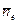 и радиуса
и радиуса 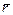 совпадают:
совпадают:  . Покажем, что коэффициент A1 в разложении j должен равняться нулю. Принимая во внимание, что расход жидкости через поверхность å согласно уравнению неразрывности равен нулю, и учитывая, что для сферы dS=R2dW, где W - телесный угол, запишем
. Покажем, что коэффициент A1 в разложении j должен равняться нулю. Принимая во внимание, что расход жидкости через поверхность å согласно уравнению неразрывности равен нулю, и учитывая, что для сферы dS=R2dW, где W - телесный угол, запишем  . Поскольку A1 и An не зависят от радиуса, а последнее равенство сохраняет свою силу и при предельном переходе R®¥, то
. Поскольку A1 и An не зависят от радиуса, а последнее равенство сохраняет свою силу и при предельном переходе R®¥, то  , т.е. A1 =0. Итак, разложения в ряд по степеням R потенциала и его производной по нормали, отвечающие физическим условиям течения, будут
, т.е. A1 =0. Итак, разложения в ряд по степеням R потенциала и его производной по нормали, отвечающие физическим условиям течения, будут
 , (5.10)
, (5.10)
откуда следует, что для твердого тела потенциал j убывает как квадрат расстояния от тела - источника возмущений, а  - как куб.
- как куб.
Если рассматривается движение тела изменяемого объема WT (t), то, поскольку при его расширении происходит вытеснение жидкости, такое тело эквивалентно нескомпенсированному источнику с расходом 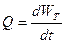 , и коэффициент A1 в разложении потенциала равен
, и коэффициент A1 в разложении потенциала равен  . Подставляя (5.10) во второй интеграл (5.8) и расширяя сферу å до бесконечности R®¥, видим, что интеграл по поверхности сферы пропадает
. Подставляя (5.10) во второй интеграл (5.8) и расширяя сферу å до бесконечности R®¥, видим, что интеграл по поверхности сферы пропадает  . Исходя из этого, выражение для кинетической энергии жидкости при безвихревом течении можно представить в виде интеграла по поверхности тела S:
. Исходя из этого, выражение для кинетической энергии жидкости при безвихревом течении можно представить в виде интеграла по поверхности тела S:
 . (5.11)
. (5.11)
В задачах, связанных с движением тела, обычно используют внешнюю к телу нормаль  . Из рис. ____ видно, что направления
. Из рис. ____ видно, что направления  и
и  противоположны. Полагая
противоположны. Полагая  , получим выражение
, получим выражение  , представляющее общую зависимость для вычисления кинетической энергии жидкости при безвихревом течении. Важно подчеркнуть, что для определения
, представляющее общую зависимость для вычисления кинетической энергии жидкости при безвихревом течении. Важно подчеркнуть, что для определения  нужно знать значения потенциала лишь на поверхности тела.
нужно знать значения потенциала лишь на поверхности тела.
Найдем выражение для потенциала вызванных скоростей j в общем случае движения тела. Функция j должна удовлетворять уравнению Лапласа. Вне тела на бесконечности согласно доказанному выше j®0. На поверхности тела должно удовлетворяться граничное условие непротекания  , где
, где  - нормальная скорость точки поверхности тела, а
- нормальная скорость точки поверхности тела, а  - нормальная скорость частицы жидкости. Представим
- нормальная скорость частицы жидкости. Представим  в развернутом виде. Пусть
в развернутом виде. Пусть  - поступательная скорость полюса, а
- поступательная скорость полюса, а  - скорость вращения тела относительно мгновенной оси, проходящей через полюс. Скорость произвольной точки поверхности тела
- скорость вращения тела относительно мгновенной оси, проходящей через полюс. Скорость произвольной точки поверхности тела 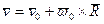 , где
, где  - радиус - вектор этой точки. Нормальная составляющая скорости точки поверхности тела
- радиус - вектор этой точки. Нормальная составляющая скорости точки поверхности тела  . Раскрывая это выражение и учитывая граничное условие, получим
. Раскрывая это выражение и учитывая граничное условие, получим
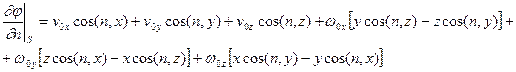 (5.12)
(5.12)
Координаты x, y, z точек поверхности S и косинусы направляющих углов в связанной с телом системе координат не зависят от времени. Функциями времени являются лишь проекции поступательной  и угловой
и угловой 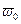 скоростей тела.
скоростей тела.
Граничное условие на поверхности тела в виде суммы шести членов и линейность уравнения Лапласа позволяют искать общее выражение для потенциала также в форме шести слагаемых
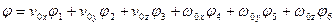 , (5.13)
, (5.13)
где 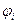 - единичные потенциалы, удовлетворяющие уравнению Лапласа
- единичные потенциалы, удовлетворяющие уравнению Лапласа  и условиям на бесконечности
и условиям на бесконечности  . Продифференцировав j по нормали, получим
. Продифференцировав j по нормали, получим
 . (5.14)
. (5.14)
Подстановка этого выражения в левую часть (12.12) показывает, что единичные потенциалы должны на поверхности тела удовлетворять граничным условиям
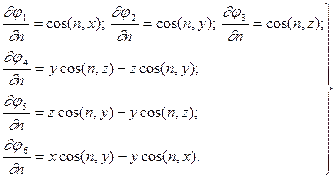 (5.15)
(5.15)
Правые части этих равенств не зависят от времени, откуда следует, что единичные потенциалы  в системе координат, связанной с телом, являются функциями только от координат.
в системе координат, связанной с телом, являются функциями только от координат.
Для упрощения последующих выкладок изменим обозначения, вводя обобщенные скорости: 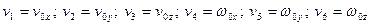 . Тогда выражение для потенциала j будет
. Тогда выражение для потенциала j будет
 . (5.16)
. (5.16)
Разделение потенциала j согласно (12.16) позволяет, таким образом, свести задачу об общем движении тела к ряду более простых задач отыскания единичных потенциалов.
Установим размерность единичных потенциалов. Поскольку [v]=м/с, [j]=м2/с, [w0]=1/c, то из сравнения размерностей левой и правой частей, получаем, что
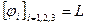 ;
;  . (5.17)
. (5.17)
Полагая, что тело движется без вращения в направлении оси x  , находим:
, находим:
j=v0xj1. (5.18)
Отсюда видно, что j1 характеризует возмущение жидкости, обусловленное поступательным движением тела в направлении оси x. Аналогично единичный потенциал j4 характеризует возмущение тела, происходящее от вращения тела относительно оси x и т.д.
Как следует из выражения (5.16) и аналогичных ему, чтобы найти единичный потенциал, нужно в выражении для j выделить множитель при обобщенных скоростях движения тела.
Вычислим кинетическую энергию жидкости. Взяв j в форме (5.16), определив  и подставив эти значения в выражение для кинетической энергии, будем иметь
и подставив эти значения в выражение для кинетической энергии, будем иметь
 . (5.19)
. (5.19)
В этой формуле множители vi как не зависящие от координат вынесены за знак интеграла и, кроме того, изменен порядок операций суммирования и интегрирования.
Вводя обозначения
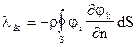 (5.20)
(5.20)
придадим выражению для  вид
вид
 . (5.21)
. (5.21)
Эта формула аналогична известной из теоретической механики зависимости для кинетической энергии твердого тела; соответственно величины  называются обобщенными присоединенными массами.
называются обобщенными присоединенными массами.
Поскольку  являются только функциями координат, обобщенные присоединенные массы согласно (12.15) не зависят от времени.
являются только функциями координат, обобщенные присоединенные массы согласно (12.15) не зависят от времени.
На основании (12.21) можно заключить, что при произвольном движении тела кинетическая энергия жидкости определяется матрицей, содержащей 36 членов
 (5.22)
(5.22)
Покажем, что для безграничной жидкости матрица кинетической энергии симметрична относительно главной диагонали
 . (5.23)
. (5.23)
Для этого достаточно показать, что 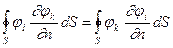 . Воспользуемся известной из математики второй формулой Грина, примененной к области W¥ между поверхностями S+å (рис.19??)
. Воспользуемся известной из математики второй формулой Грина, примененной к области W¥ между поверхностями S+å (рис.19??)  . Поскольку единичные потенциалы
. Поскольку единичные потенциалы  и
и  удовлетворяют уравнению Лапласа Dji =0 и Djk =0, левая часть этого равенства обращается в нуль. Устремляя поверхность S в бесконечность, аналогично предыдущему, можно показать, что интеграл в правой части по S исчезает, и последнее выражение принимает вид
удовлетворяют уравнению Лапласа Dji =0 и Djk =0, левая часть этого равенства обращается в нуль. Устремляя поверхность S в бесконечность, аналогично предыдущему, можно показать, что интеграл в правой части по S исчезает, и последнее выражение принимает вид  . Заменяя здесь
. Заменяя здесь 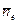 на
на  , приходим к свойству симметрии матрицы присоединенных масс, т.е. число независимых обобщенных присоединенных масс сокращается до 21.
, приходим к свойству симметрии матрицы присоединенных масс, т.е. число независимых обобщенных присоединенных масс сокращается до 21.
Установим размерность обобщенных присоединенных масс  с индексами 1, 2, 3. Поскольку
с индексами 1, 2, 3. Поскольку 
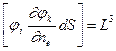 , то размерность величин
, то размерность величин 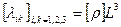 , т.е. они имеют размерность массы. Отметим, что при
, т.е. они имеют размерность массы. Отметим, что при  , величины присоединенных масс l11, l22, l33 всегда положительны.
, величины присоединенных масс l11, l22, l33 всегда положительны.
Если i =1,2,3, k=4,5,6, то  , [jk]=L2. Аналогично предыдущему устанавливаем, что
, [jk]=L2. Аналогично предыдущему устанавливаем, что  . В этом случае члены
. В этом случае члены  имеют размерность статического момента.
имеют размерность статического момента.
Если i,k =4,5,6, 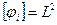 , то
, то  , т.е. размерностями этих величин являются моменты инерции. При
, т.е. размерностями этих величин являются моменты инерции. При 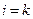 величины l44, l55, l66 положительны; знаки
величины l44, l55, l66 положительны; знаки  при
при  могут быть различны в зависимости от формы тела.
могут быть различны в зависимости от формы тела.
В практических расчетах обычно применяют следующие безразмерные коэффициенты присоединенных масс  :
:
а) для  с размерностью массы (i,k =1,2,3)
с размерностью массы (i,k =1,2,3)
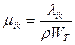 , (5.24)
, (5.24)
где rWT - масса жидкости в объеме тела;
б) для  с размерностью статического момента (i=1,2,3, k=4,5,6)
с размерностью статического момента (i=1,2,3, k=4,5,6)
 , (5.25)
, (5.25)
где L1 - характерный линейный размер;
в) для  с размерностью момента инерции (i,k=4,5,6)
с размерностью момента инерции (i,k=4,5,6)
 , (5.26)
, (5.26)
где L2 - характерный линейный размер. В случае присоединенных моментов инерции с одинаковыми индексами  под L2 понимают радиус инерции масс жидкости в объеме тела.
под L2 понимают радиус инерции масс жидкости в объеме тела.
Можно показать, что у тела с одной плоскостью симметрии число обобщенных присоединенных масс сокращается до 12. Так, если плоскостью симметрии служит плоскость 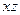 , то l12= l14= l16=l23= l25= l34=l36= l45= l56= 0.
, то l12= l14= l16=l23= l25= l34=l36= l45= l56= 0.
Рассмотрим принцип доказательства равенства (12.27) на примере вычисления l12. Обозначая через S1 и S2 верхнюю и нижнюю части поверхности тела, которые симметричны относительно плоскости 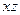 , и используя (5.15), получим
, и используя (5.15), получим
 .
.
В сходственных точках A1 и A2 поверхностей S1 и S2 единичный потенциал j1, характеризующий возмущение при движении в направлении оси x, имеет одинаковые значения j1(S1) = j1(S2), а знаки направляющих косинусов различны. На основании этого заключаем, что интегралы от этой функции по одинаковым поверхностям S1 и S2 взаимно сократятся. Таким образом, l12 =0.
У тела, симметричного относительно двух плоскостей (например, тело с плоскостями симметрии 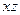 и
и  ), остается лишь восемь присоединенных масс l11, l22, l33, l44, l55, l66, l26, l35.
), остается лишь восемь присоединенных масс l11, l22, l33, l44, l55, l66, l26, l35.
Примером может служить дублированное тело, получаемое сложением по плоскости ватерлинии (плоскость симметрии) подводных объемов судна. Вторая плоскость симметрии - диаметральная. Подобное допущение принимается при исследовании вопросов управляемости судна, движущегося на свободной поверхности без учета волнообразования.
У тела, симметричного относительно трех плоскостей симметрии (трехосный эллипсоид), l26= l35= 0 и остается шесть присоединенных масс l11, l22, l33, l44, l55, l66.
Если тело является телом вращения с продольной осью x, то по соображениям симметрии, учитывая, что вращение тела относительно оси x в невязкой жидкости не вызывает возмущений в жидкости, l22=l33; l55= l66; l26=l35; l44=0.
Для плоской задачи, т.е. при движении контура в плоскости  , обращаются в нуль проекции скоростей v3=v0z, v4=w0x, v5=w0y и, следовательно, не равны нулю лишь l11, l22, l12, l16, l26 и l66.
, обращаются в нуль проекции скоростей v3=v0z, v4=w0x, v5=w0y и, следовательно, не равны нулю лишь l11, l22, l12, l16, l26 и l66.
Поиск по сайту: