Теорема стокса о связи интенсивности с циркуляцией

Теорема Стокса. Циркуляция скорости по любому замкнутому контуру L равна интенсивности вихрей, пронизывающих произвольную поверхность S, опирающуюся на этот контур.

Для доказательства поместим в вихревой поток элементарный прямоугольный контур 12341 (рис.4) со сторонами dx и dy и подсчитаем циркуляцию скорости по нему. На рис.4 показаны касательные к контуру составляющие скорости для каждой стороны. Так как длина сторон контура мала, можно считать скорости вдоль каждой стороны постоянными.

Для стороны 12 касательной будет скорость V_x, а для 41 - V_y, взятые в точке 1.

Для стороны 23 в качестве касательной примем скорость . Слагаемое показывает изменение скорости в точке 2 по сравнению с точкой 1.

Аналогично для стороны 34 касательная скорость будет иметь вид .

Подсчет циркуляции начнем с точки 1, тогда

Два последних слагаемых записываются со знаком минус, так как скорость на участках 3-4 и 4-1 направлена против положительного направления обхода контура при подсчете циркуляции. Приведя подобные члены в последнем уравнении, его можно представить в виде

.

Сравнивая выражение, стоящее в скобках, с выражением для угловой скорости [1]

,

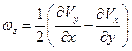вместо предыдущего равенства можно записать

.

Так как - элементарная площадка dS, ограничиваемая рассматриваемым контуром, и она нормальна к составляющей угловой скорости (см. рис.4), в правой части последнего равенства записана элементарная интенсивность dJ (1.2), т.е.

. (1.5)

Значит, циркуляция скорости по элементарному контуру равна интенсивности вихря, пронизывающего элементарную площадку, ограниченную этим контуром.

Распространим полученный результат на произвольный плоский контур конечных размеров L (рис.5). Для этого разобьем его на ряд элементарных контуров. Суммарная интенсивность вихрей, пронизывающих поверхность, ограниченную рассматриваемым контуром, равна сумме элементарных интенсивностей вихрей dJ, пронизывающих элементарные площадки, т.е. 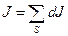. Так как (1.5), последнее равенство можно продолжить

.

Из рис.5 видно, что циркуляции по общей стороне соседних элементарных контуров одинаковы по абсолютной величине (так как сторона одна и та же) и противоположны по знаку (направление обхода различно), соответственно их суммы попарно равны нулю. В результате сложения циркуляций по всем элементарным контурам останется лишь сумма циркуляции по внешнему контуру L. В результате можно записать, что по контуру L, а, следовательно,

, (1.6)

что и следовало доказать.

Последняя формула справедлива и для неплоских, пространственных поверхностей, опирающихся на произвольный контур.

Практическое значение теоремы Стокса заключается в том, что измерив и вычислив циркуляцию по замкнутому контуру, можно судить об интенсивности вихревого движения жидкости в потоке.

Поиск по сайту: