Теорема Гельмгольца о вихрях. Формы существования вихрей

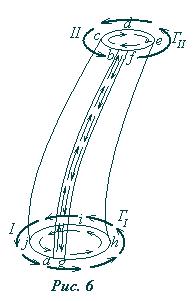Рассмотрим часть вихревой трубки (рис.6). Мысленно разрежем ее вдоль вихревой линии и слегка раздвинем по разрезу, после чего запишем выражение для циркуляции скорости по полученному контуру abcdefghija, оставляя, как это положено, поверхность, ограниченную этим контуром слева при обходе (тонкие стрелки на рис.6). Так как рассматриваемая поверхность является боковой поверхностью вихревой трубки, состоящей из вихревых линий, ни один вихрь не проходит сквозь нее (т.к. параллельна dS в каждой точке) и интенсивность вихрей, пронизывающих эту поверхность, равна нулю. В соответствии с теоремой Стокса, циркуляция по контуру, на который опирается эта поверхность, также равна нулю,

.

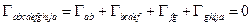Циркуляция скорости на участках ab и fg равны по абсолютной величине, но противоположны по знаку и в сумме дают ноль, взаимно уничтожаясь. Тогда последнее равенство можно записать в виде

. (1.7)

Теперь рассмотрим циркуляцию скорости по контурам I и II, ограничивающим концевые сечения рассматриваемой вихревой трубки. Положительное направление их обхода показано на рис.6 толстыми стрелками. Из рисунка видно, что , а . Тогда вместо (1.6) можно записать

.

Применяя теорему Стокса для сечений I и II вихревой трубки (,а ), окончательно получим

. (1.8)

Выражение (1.8) характеризует кинематическую теорему Гельмгольца, которая, если учесть, что сечения I и II вихревой трубки были выбраны произвольно, можно сформулировать так: интенсивность вихря постоянна по его длине.

Как при доказательстве теоремы Стокса, так и при доказательстве теоремы Гельмгольца, нигде не были седланы оговорки о характере жидкости. Поэтому обе теоремы справедливы как для невязкой, так и для реальной, вязкой жидкости. Так как интенсивность вихря остается постоянной по его длине. Он не может кончиться в жидкости. В самом деле, если предположить, обратное, т.е.что площадь его поперечного сечения стала равной нулю, а интенсивность его по-прежнему постоянная и конечная величина в соответствии с теоремой Гельмгольца, мы неизбежно придем к теоретическому выводу на основании формулы для интенсивности (1.3) (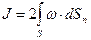), что w стала равной бесконечности, чего физически не может быть. Значит, вихрь не может кончиться в жидкости, а отсюда следуют возможные формы существования вихрей, показанные на рис.7. Как видно, вихрь может кончиться на твердой стенке или свободной поверхности. Кроме того, возможен вариант, когда вихрь замыкается сам на себя, образуя вихревое кольцо. В теории крыла рассматриваются так называемые полубесконечные вихри, которые начинаются на твердой стенке и уходят в теоретически в бесконечность. На самом деле из-за увеличения поперечных размеров вихря, угловая скорость вращения и он «размывается» в потоке жидкости, в то время как энергия вихря превращается в тепло.

Как показано в теории вихрей, в невязкой жидкости вихрь может существовать неограниченно долго. В вязкой же жидкости интенсивность вихря из-за трения постепенно уменьшается, оставаясь, впрочем, постоянной по длине в каждый момент времени в соответствии с рассмотренной теоремой Гельмгольца.

В реальной жидкости вихревые движения распространены очень широко: от вихрей в атмосфере до течения жидкости в трубах, около твердых стенок и пр. Теория вихревого движения используется в теории крыла, в расчетах гребных винтов и многих других разделах прикладной гидромеханики.

Поиск по сайту: