Плоский источник (сток)

Под плоским источником понимается поток жидкости, равномерно вытекающий во все стороны из каждой точки бесконечно длинной прямой линии. Физической интерпретацией такого потока может служить истечение воды из длинной и тонкой дренированной трубы. При таком движении жидкости картина течения в каждой плоскости, перпендикулярной рассматриваемой линии, будет одинакова. Это течение является плоскопараллельным течением и может рассматриваться только в одной плоскости.

Найдем расход жидкости через круговую цилиндрическую поверхность, осью которой является источник, расположенный в начале координат (рис.10,а). Если цилиндрическая поверхность имеет радиус r, расход жидкости через ее отрезок единичной длины можно записать в виде

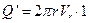
Через любую круговую цилиндрическую поверхность, осью которой является источник, протекает то же количество жидкости (по закону сохранения расхода жидкости, если жидкость в области вокруг источника не исчезает и не появляется из других источников).

Обозначим количество жидкости, вытекающей из источника единичной длины, которое называется интенсивностью источника, через Q:

, ,

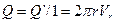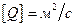тогда скорость потока на расстоянии r от источника равна

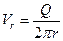. (2.6)

Подставляя (2.6) в формулы (2.3), можно записать

.

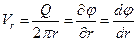Здесь частная производная заменена полной, так как скорость потока от источника зависит только от радиуса окружности. При этом можно записать последнее равенство в виде

,

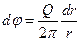что после интегрирования и отбрасывания постоянной C даст потенциал плоского источника

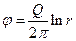. (2.7,а)

Течение, обратное плоскому источнику, когда жидкость из окружающей среды равномерно подтекает к некоторой линии, называется плоским стоком (рис.10,б). При таком течении скорость имеет обратное направление

,

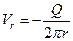а потенциал скорости течения плоского стока имеет вид

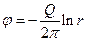. (2.7,б)

Несложно показать, что если источник (сток) расположен не в начале координат, а в произвольной точке (x₁, y₁, z₁), то формулы (2.7) и (2.8) примут вид

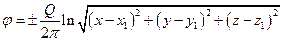. (2.8)

Поиск по сайту: