ВКЛАД Эйлера в РАЗВИТИЕ тригонометрии

Понятно, что столь ярко выраженный аналитический гений, каким являлся Эйлер, раз занявшись вычислительной тригонометрией, должен был значительно продвинуть ее вперед. Повод обратиться к тригонометрии представился ему в уже неоднократно упоминавшемся «Введении в анализ» (1748). В восьмой главе его первого тома Эйлер впервые ввел в анализ угловые функции как числовые величины, с которыми можно производить вычисления, как со всякими другими, так, чтобы впредь они уже не оказывали влияния на размерность выражений. И хотя Эйлер и не определил нигде тригонометрические функции явно как отношения сторон прямоугольного треугольника, но всегда рассматривал их именно так. Если отвлечься от несущественных мелочей, то изложение и символика Эйлера были вполне современными. Уже в одной работе в 1729 (1735) он записал теорему косинусов сферической тригонометрии в виде

cos: ВС = cos: АВ • cos: AC + cos A • sAB • sAC;

целый синус, который все еще употребляло большинство прежних авторов, здесь уже был принят равным 1. Обозначения тригонометрических функций во «Введении» были таковы: sin. A. z или sin. z (A = arcus), cos. A. z или cos. z, tang. z, cot. z и т. д.

В начале названной главы были впервые систематически установлены формулы для sin (z + 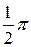), sin (z+p) и т. д. Написав:

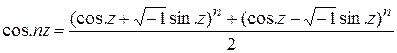
Эйлер раскрыл скобки и получил таким путем формулу для cosnz; аналогично он нашел формулу для sinnz. Беря п бесконечно большим, a z бесконечно малым, так что cosz=l и sinz=z, он вывел из этих формул бесконечные ряды для синуса и косинуса. Отсюда он получил ряды для синуса, косинуса, тангенса и котангенса 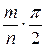, отчасти опубликованные им уже в Comm. Ac. Petr., 1739 (1750). Затем он исчерпывающим образом показал, как можно использовать эти ряды для вычисления тригонометрических таблиц. Позднее в Nov. Comm. Ac. Petr., 1754/55 (1760) он вывел дальнейшие ряды для sinⁿj, cosⁿj, sin^mj, cosⁿj, следующие по функциям углов, кратных j. На связь между показательной и тригонометрическими функциями Эйлер натолкнулся уже в одной работе о рядах, помещенной в Comm. Ac. Petr., 1740 (1750). Соответствующую определяющую формулу для синуса он дал в Misc. Berol., 1743, но доказаны были формулы для синуса и косинуса только во «Введении». О результатах Эйлер, очевидно, ничего не знал. Формулы

cos х = 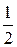(e^ix + e^-ix) и sin x = 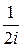(e^ix — e^-ix)

он получил во «Введении» из выражени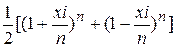й

и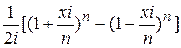

полагая п = ¥. К этому он присоединил еще формулу

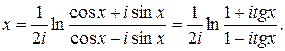
Определение sin(x+iy) и cos(x+iy) он впервые дал в 1749.

Суммирование рядов синусов и косинусов, аргументы которых растут в арифметической прогрессии, Эйлер произвел уже в 1748. Во «Введении» он вновь вернулся к этому вопросу с более общей точки зрения. Позднее (Петербург, 1783) он занялся аналогичными рядами, аргументы которых образуют геометрическую прогрессию. Представлением тригонометрических функций в виде произведений Эйлер начал заниматься уже в 1734-35 (1740), где разложил в бесконечное произведение синус. То же самое он провел для синуса и косинуса 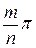в 1740 (1750). Все это вместе с некоторыми дополнениями было включено во «Введение», в 14-й главе которого он также детально занялся вопросом об умножении и делении углов, т. е. о тригонометрических функциях кратных углов. Мы указывали в первой части, что в этих разнообразных исследованиях Эйлер действовал более творчески, нежели критически. Это столь глубоко коренилось в его натуре, что он оставил без внимания возражения, сделанные ему главным образом Николаем I Бернулли уже в 1742 и 1743. Эйлер продолжал производить вычисления над любыми бесконечными рядами, распространял теоремы о конечных многочленах на бесконечные и придавал любые значения индексу п, в начале доказательства считавшемуся целочисленным. Несмотря на это, получаемые им результаты обычно бывали справедливы, хотя в некоторых случаях он пришел и к ошибочным выводам, как, например, в упоминавшейся статье в Nov. Comm. Ac. Petr., 1754-55 (1760).

Во втором томе «Введения» (глава 22-я) Эйлер применил к решению трансцендентных уравнений, вроде s=cos s или s=sin 2s и т. п., правило ложного положения. Как сообщает он сам, он придумал подобные задачи с целью посмотреть, нельзя ли приблизиться таким путем к квадратуре круга. Позднее, когда Ламберт уже доказал иррациональность p, Эйлер вновь занялся подобными рассмотрениями, подчеркивая, что работа Ламберта отнюдь еще не доказала невозможность квадратуры круга.

Прежде чем перейти к заслугам Эйлера в сферической тригонометрии, упомянем еще о двух тригонометрических разложениях, лежащих несколько в стороне. Эйлер нашел их, развивая предложенный Декартом и затем неоднократно открывавшийся вновь способ построения окружности данной длины (Декарт, Амстердам, 1701). Это бесконечный ряд

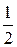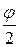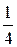tgj + tg + tg 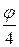+...= 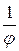- 2ctg2j

и бесконечное произведение

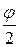cos jcos cos ... = ,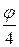

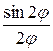которое Эйлер другим путем вывел уже в 1737 (1744).

Сферической тригонометрией Эйлер специально занялся в двух больших статьях, подойдя при этом к ней с различных точек зрения. В первой, помещенной в Mem. Ac. Berl., 1753 (1755) он совершенно общим образом построил сферическую тригонометрию как геометрию треугольников, составленных на поверхности сферы линиями кратчайшего расстояния. Эйлер исходил из прямоугольного треугольника, обозначив катет АР через х, катет РМ через у, гипотенузу AM через s [рис. 4]. Если О — полюс большого круга (экватора), на котором лежит АР, а Ор — меридиан, бесконечно близкий к ОР, то

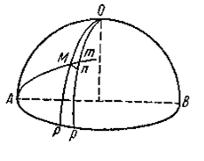
Mm = ds, mn = dy, Pp = dx

и линия Мп, лежащая на параллельном круге широты у, равна dxcosy, так что

ds = Ö .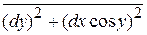

Далее, Эйлер искал условия, при которых интеграл этого элемента дуги будет иметь минимальное значение, и получил, таким образом, 10 уравнений, возникающих из правила Непера. Здесь в первый раз появились обозначения, которые мы теперь склонны считать само собой разумеющимися и отсутствие которых часто придавало такой неудобный вид прежним работам. Мы имеем в виду обозначение трех сторон буквами а, b, с, а противолежащих вершин и углов треугольника буквами А, В, С. То, что мы обозначаем последние по большей части буквами а, b, g, конечно, менее существенно. Греческие буквы были введены лишь в XIX столетии, хотя иногда а, b, g, применялись уже А. Кестнером в его «Основаниях арифметики, геометрии и тригонометрии» (Геттинген, 1759; 6-е изд. 1800). Новые обозначения позволили Эйлеру записать свои десять уравнений вполне в современном виде. Затем он получил из них шесть различных основных уравнений для прямоугольного треугольника. Соответствующим образом Эйлер поступил и в случае общего сферического треугольника. Определив минимум одной из сторон, он прежде всего нашел пять фундаментальных уравнений, из которых затем вывел теорему синусов, обе теоремы косинусов и так называемое правило котангенса (впервые встречающееся у Виета); последнее появилось у него в форме

sin a tg С — sin В tg с = cos a cos B tg C tgc,

переходящей в употребляемую ныне при делении на tgCtgc. Эйлер записывал каждую теорему в трех видах, которые получаются друг из друга циклической перестановкой, хотя сам Эйлер ею не пользовался. О полярном треугольнике Эйлер не упоминал, и вообще, с точки зрения полноты, в статье имелось несколько малозначительных пробелов. Зато применения и преобразования фундаментальных теорем были в высшей степени богатые.

Среди прочего материала здесь имелись все формулы для половинных углов, правда, без сокращенных обозначений полусумм сторон и углов, затем четыре аналогии Непера—Бригса, употребление вспомогательного угла в теореме косинусов, причем последняя приводилась еще в новой форме:

cos a =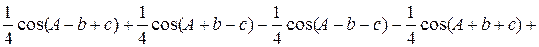

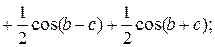
сообщалась и формула, полярная с приведенной.

Прибавим, что вслед за этой статьей Эйлер в том же томе Mem. Ac. Berl. поместил работу, подробно излагавшую тригонометрию на поверхности сфероида, особо учитывая вопросы, связанные с измерением земли. Аналогичные исследования были произведены позднее дю-Сежуром [1778 (1781)].

Во второй статье по сферической тригонометрии [1779 (1782)] Эйлер принял для построения системы ее формул элементарную основу. Он исходил здесь из трехгранника, который пересекал соответствующими плоскостями, с тем, чтобы после применить теоремы плоской тригонометрии (подобно Копернику). Он вывел, таким образом, теорему синусов, теорему косинусов для сторон и новую формулу, связывающую пять элементов:

cos A sin с = cos a sin b — sin a cos b cos С,

отметив, что эти три формулы содержат в себе всю сферическую тригонометрию. Полученное здесь третье уравнение Эйлер подверг неоднократным преобразованиям. Он вывел из него так называемую формулу котангенсов, теорему косинусов для углов и, с помощью теоремы синусов, полярную с ней формулу. Лишь после этого он ввел полярный треугольник и объяснил его способ применения, привел, частично выведя их по-новому, логарифмические формулы и с полным правом заявил, что его статья дает полное изложение системы сферической тригонометрии.

1.5. последователи Эйлера а развитии тригонометрии

В числе последователей Эйлера имелся ряд выдающихся математиков. Особенно многое сделал в области сферической тригонометрии петербургский академик А. И. Лексель. Он показал, что геометрическим местом вершин всех треугольников с общим основанием и равной площадью является малый круг и что произведения синуса стороны (или, соответственно, угла) и соответствующей высоты имеют постоянную величину d. И с помощью этих равенств, представляющих собой обобщения формулы Герона, он вывел изящные выражения для тангенсов сферических радиусов вписанного в треугольник и описанного кругов, установил формулы для cos ½ (A ± B ± C), доказал теорему, соответствующую в сферическом четырехугольнике, вписанном в круг, теореме Птолемея, распространил на шар еще некоторые другие предложения планиметрии.

Ряд статей по сферической тригонометрии опубликовали два

других петербургских академика — Н. Фус и Шуберт. И. Т. Майер младший дал логарифмическую трактовку плоской теоремы косинусов («Капитальный курс практической геометрии», т. 1,Геттинген, 1777). Следует упомянуть и Кестнера с его «Геометрическими статьями» (1790/91), хотя он все еще употреблял целый синус. Неудачным в отношении формы было также построение сферической тригонометрии, данное в 1783 (1786) Ж. П. де-Гюа.

Лагранж содействовал успехам тригонометрии, применив к непосредственному решению уравнений ряды, что было особенно важно для практических целей астрономии и геодезии. Oн решил с помощью мнимых величин гониометрическое уравнение tg x = m tg y относительно х. Это уравнение он связал с формулами для прямоугольного треугольника и с аналогиями Непера. Подобные разложения в ряды встречались, впрочем, еще у Ламберта.

Превосходной книгой, имевшей в романских странах почти такое же значение, как учебник Клюгеля в германских, оказалась опубликованная впервые в 1786 «Плоская и сферическая тригонометрия» (итальянское и французское издание, Париж) Каньоли. Каньоли производил вычисления все еще над тригонометрическими линиями, но радиус круга брал равным единице, и если он не перенял обозначения элементов треугольника, введенные Эйлером, то вообще примкнул к нему полностью и всю свою работу построил на аналитической основе. Несмотря на то, что в этом направлении сделано было уже многое, ему все же удалось в ряде пунктов внести некоторые усовершенствования. Стоит упомянуть о его приведении к логарифмическому виду с помощью вспомогательного угла плоской теоремы косинусов (по способу Майера), а также сферической теоремы косинусов. Bывод новых формул для сферических прямоугольных треугольников, имевших назначением ббльшую точность вычислений, и далее установление изящных формул, связывающих элементы сферического треугольника с элементами соответствующего ему треугольника, составленного из хорд. Независимо от Кестнера, Каньоли решил уравнение a cos А + b sin А = n с помощью подстановок а = т cos В и b = т sin В, он добавил важное отношение между шестью элементами сферического треугольника: sin с sin a + cos с cos a cos В = sin A sin С — cos A cos С cos b, а также вывод суммы тригонометрического ряда, причем распространил суммирование на случай n-х степеней таких функций.

С. Лакруа в своем «Элементарном курсе прямолинейной и сферической тригонометрии и т. д.» (Париж, 1798/99) в противоположность Каньоли ввел символику Эйлера, но зато почти всюду сохранил в формулах R.

К изложению непосредственных успехов тригонометрии мы присоединим краткий обзор формы, которую постепенно приняла система тригонометрии в учебниках. Мы неоднократно отмечали, что, за исключением Клюгеля, все прочие авторы еще вводили в качестве целого синуса радиус г, отчасти, правда, лишь с целью удовлетворить все еще сохранявшуюся потребность в однородности выражений. Только для упрощения формул часто г полагался равным единице. Отнюдь не было еще усвоено большинством математиков и определение знаков отрезков. Поэтому знаки функций углов, бoльших 90°, отчетливо устанавливались лишь при помощи гониометрических формул, причем для тангенса особенно важной являлась пропорция

tg a: r= sin a: cos a

Эта форма пропорции, а также применение радиуса г, часто продолжали сохраняться и в других случаях даже в XIX столетии. Зато получило почти всеобщее распространение современное обозначение функций, данное Эйлером. В больших книгах, вроде «Начал геометрии» (1794) Лежандра, «Теоретической математики» (Росток, 1760) и «Системы математики» Карстена, функции отрицательных аргументов рассматривались совершенно правильно, начало чему положило уже «Введение в анализ» Эйлера.

Гониометрические формулы еще часто выводились каждая сама по себе и притом геометрически. Правда, Лежандр и Каньоли вывели основные формулы из теоремы сложения, но только Клюгель ясно выразил основоположное значение этой теоремы. Обосновать самую теорему сложения и для углов, бoльших 90°, счел необходимым один Лежандр. «Высшую тригонометрию» включил в свою работу, кроме Клюгеля, также еще Каньоли. Также поступили Карстен, А. Р. Модюи в своих «Началах сферической астрономии и т. д.» (Париж, 1765), а в особенно широком объеме Л. Бертран во втором томе своего труда, вышедшего под названием «Новое изложение элементарной части математики» (Женева, 1778).

Обозначение углов, предложенное Эйлером, переняли только Клюгель и Кестнер. У других авторов, в силу отсутствия единообразной символики, формулы были ненужным образом усложнены. Наиболее полная система формул для плоского треугольника, включая так называемые уравнения Молльвейде, выведенная при этом совсем по-современному, имелась у Каньоли. Однако даже вычисление плоских прямоугольных треугольников получило современный простой вид только в XIX столетии, когда отказались от целого синуса.

Сферическая тригонометрия излагалась в учебниках почти сплошь аналитически. Исключением явилась «Trigonometrie spherique» (Париж, 1757) С. Валетта, который примкнул к «Построению сферической тригонометрии» Бошковича, нашел заново все, что входило в «Аналемму» Птолемея, и графически развил всю сферику. Во всех остальных книгах и после выхода второй работы Эйлера сначала устанавливались все формулы для прямоугольного треугольника, а затем отдельно рассматривался косоугольный треугольник, который для этого разбивался с помощью высоты на два прямоугольных. Применение теорем к составляющим прямоугольным треугольникам давало после исключения высоты систему пяти уравнений, имевшуюся еще в «Началах арифметики и геометрии» (1739) Зегнера и перешедшую во все.

В заключение мы сжато рассмотрим попытки построить всю тригонометрию на возможно более простой основе. Уже Кестнер в позднейших изданиях «Оснований» (например, 3-е изд., 1774) вывел главные формулы тригонометрии из теоремы синусов и того, что А + В + С= 180°, а Оппель еще ранее показал, как можно получить все формулы сферической тригонометрии из теорем синусов и косинусов. Еще ранее Ф. К. Майер указывал на возможность достигнуть этого с помощью одной лишь теоремы косинусов. Осуществил эту возможность только де-Гюа.

Лагранж, начавший с того же, что и де-Гюа, благодаря значительно более искусному обращению с формулами, впервые придал выводу всех прочих тригонометрических равенств современный вид (1798/99). Прежде всего он доказал соотношение Эйлера. Столь же просто вывел он и правило котангенса. Лагранж подчеркивал, что с помощью этих четырех формул можно решить любую задачу, однако он также вывел, постоянно пользуясь полярным треугольником, все остальные известные уже нам формулы. Статья Лагранжа представляла собой достойное увенчание успехов тригонометрии на пороге XIX столетия.

Поиск по сайту: