ТригонометриЯ В ЕВРОПЕ до Эйлера

Оказавшийся столь важным для развития учения о геометрических местах 1637 год не имел такого же значения для элементарной геометрии. В частности, сам Декарт ничего не сделал для тригонометрии как таковой. Как в его «Геометрии», так и в комментариях к ней тригонометрические функции углов фигуры выражались через отношения сторон связанных с ней прямоугольных треугольников.

Тем не менее тридцатые годы XVII столетия завершили в известной мере построение тригонометрии: мы имеем в виду создание логарифмических методов вычислений. Отметим, что в 1633 вышла «Британская тригонометрия» Бригса—Геллибранда, содержавшая во второй части наиболее употребительные приемы решения плоских и сферических треугольников, с учетом в первую очередь формул логарифмического характера. Наряду с аналогиями Непера Геллибранд применял формулы, определяющие половину угла по трем сторонам как для плоского (Ретик, ранее 1576, опубликовано в 1596), так и для сферического треугольника (Непер в Constructs, 1619). Случай трех данных углов в сферическом треугольнике Геллибранд приводил, впрочем, с помощью полярного треугольника к случаю трех данных сторон, не сообщая никаких формул. В таблицах, составлявших первую часть «Британской тригонометрии», авторы ввели десятичное деление градуса. Однако в опубликованной одновременно работе «Искусственная тригонометрия» Флакк снова пользовался старым шестидесятеричным делением и образовал тем самым основу всех позднейших таблиц.

Укажем еще на книгу Крюгера «Употребление логарифмической тригонометрии» (Данциг, 1634), принадлежащую также и к разбираемому нами периоду, поскольку новые издания ее вышли в 1648 и 1654. Крюгер применял неперовы аналогии в случаях сферических треугольников с данными a, b, f и а, р, с вполне по-современному. Для плоского треугольника с тремя данными сторонами а^>Ь^>с он привел длинное словесное указание, которое в наших обозначениях гласит, что прежде всего нужно определить вспомогательную величину х из уравнения

а затем из уравнения

найти угол β и из уравнения

угол γ. Здесь х обозначает разность р — q проекций сторон b, с на ВС. Этот обход теоремы косинуса был характерен для всей тогдашней английской тригонометрии (соответствующие чертежи имелись, например, у Оутреда и Дж. Ньютона. Восходил он к Descriptio Непера и основывался, по существу, на теореме о том, что

которая была известна в различных формах еще древним грекам и арабам.

Как в алгебре, так и в тригонометрии нового времени прежде всего усовершенствована была форма. И здесь и там совершался постепенный переход от античного изложения с помощью пропорций и нередко длинных вычислительных рецептов к алгебраическому исчислению и уравнениям. В значительной мере этот прогресс был осуществлен теми же учеными. П. Эригон распространил свою символику и на тригонометрию. В качестве образца мы приведем лишь форму, в которой он изложил теорему косинусов для плоскости. Нужно заметить при этом, что на чертежах Эригона в вершинах углов стояли большие буквы, которые часто сами обозначали эти углы, а в тексте — малые, и что D представляет собой основание высоты, проведенной из А. Теорема имела у Эригона следующий вид:

В Англии весьма способствовал более символическому изложению тригонометрии

В сочинении Оутреда были даны первые (геометрические) доказательства обеих аналогий Непера. Непер, а также Бриге и Геллибранд опубликовали только самые формулы, притом в логарифмическом виде.

Аналитический вывод неперовых аналогий дал впервые Джон Ньютон в большом труде «Британская тригонометрия» (Лондон, 1658). Впрочем, этот вывод, как и другие доказательства вычислительного характера, приведенные Ньютоном, был еще весьма громоздким. Сочинение Дж. Ньютона представляло собой значительно улучшенное и дополненное новое издание одноименной работы Бригса — Геллибранда. В нем, как и в несколько более ранней «Британской астрономии» того же автора (Лондон, 1656), впервые регулярно употреблялись термины «косинус» и «котангенс». Для «синуса», «тангенса» и «секанса» это сделал еще Т. Финк 1583, так что теперь наименование тригонометрических функций было уже установлено, хотя и не стало пока общеупотребительным.

Упомянем здесь, что формулы, выражающие функции удвоенного угла через функции однократного), были в это же время дополнены формулой, записываемой в наших обозначениях в виде:

Эту теорему привел Джон Пелль в своей книге «Споры об истинном измерении круга» (Амстердам, 1647); там же она была доказана различными способами Робервалем и другими математиками. Более общее правило для tg(a+β) и, кроме того, для sc (a+β) впервые вывел (геометрически) Я. Герман в Acta Erud., 1706. Забегая вперед, добавим, что формула

появилась лишь во «Введении» Эйлера (1748) и что важные формулы, позволяющие рационально выразить sin 2а и cos 2а через tg a, были установлены еще позднее И. Ламбертом в первой книге его «Очерков об употреблении математики», 1765.

Задачу об определении двух углов (β и γ) треугольника по третьему углу а и логарифмам сторон Ь и с впервые решил по словам Томаса Стрита (Astronomia Carolina, Лондон, 1661) Роберт Андерсон, введший для этой цели вспомогательный угол. Он, в переводе на наши обозначения, положил tg j = b/c, вычислил j и затем определил угол β-γ:

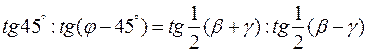
Теорема была передана словесно; доказательство, предполагавшее известной теорему тангенсов, имело сложный геометрический характер. Отсюда этот прием перешел в большинство учебников.

Из энциклопедических изложений тригонометрии заслуживает упоминания благодаря ее большой ясности «Тригонометрия» (в книге II «Astronomia Britannica», Лондон, 1669) В. Уинга. Уинг опирался на Непера, Норвуда. Для каждого случая он приводил пример, вычисленный с помощью логарифмов, но иногда опускал доказательства. Случай сферического треугольника с тремя данными сторонами был разобран Уингом на основе формулы

как это нередко делали в то время вслед за Непером. Уинг пользовался сокращениями s., cs., t., ct. В «Компендии математики» (A mathematical Compendium, Лондон, 1674), составленном на основании заметок Дж. Мура, Н. Стефенсон писал S., Cos., Т., Cot., но иногда производил сокращения и по-другому (si:, si. со., cos и т. д.). Дж. Валлис в «Трактате об угловых сечениях» пользовался для обозначения синуса, косинуса, тангенса и котангенса соответственно буквами S, £, Т и т. С помощью этих обозначений он впервые придал основным формулам гониометрии вид уравнений

Нам чужды лишь «целый синус» (R), который долгое время еще продолжали применять, а также употребление функций секанса, косеканса, синус-верзуса (1 — cos) и синус-верзуса дополнительного угла.

В то время как у самого Валлиса эти немаловажные новшества играли скорее подчиненную роль (ибо в печати он применил их лишь в одной небольшой статье), Джон Кесуэлл, опираясь на них, составил «Плоскую и сферическую тригонометрии», которая также вышла в приложении к «Алгебре» Валлиса и в которой мы видим первое, более насыщенное формулами, изложение тригонометрии. В этой работе, например, формулы половинных углов по трем сторонам плоского треугольника были впервые выведены с помощью алгебраического преобразования теоремы косинусов. Большой прогресс в приемах Кесуэлла становится особенно ясным, если сравнить с его выводом громоздкие геометрические доказательства тех же формул, которые дал в своих «Математических этюдах» (кн. V) Ф. Скаутен.

Теорему косинусов сферической тригонометрии Кесуэлл вывел из трехгранника, накладывая боковую грань на основание. По-видимому, это был первый случай вывода тригонометрических формул с помощью методов начертательной геометрии. Затем Кесуэлл алгебраически преобразовал теорему, причем получил формулы сферической тригонометрии для половинных углов.

Обозначив основание треугольника, как и Оутред, через В, боковые стороны через m, n, полупериметр через x¹), он, например, нашел для тангенса половины угла при вершине пропорцию

которая без труда переходит в современную форму

Неперовы аналогии Кесуэлл сначала доказал искусственным образом геометрически, но затем он привел четыре теоремы из наследия священника Томаса Бекера, которые аналитически вывел из обычных теорем для прямоугольного треугольника и из которых затем получил с помощью выкладок также аналогии Непера.

Первой графически изображена была функция синуса. Роберваль вычертил ее график в связи с определением площади циклоиды. Именно, он начертил внутри циклоиды и на ее основании, с помощью закрепленного в левом конце основания образующего круга, линию, названную им Trochoidis comes (или также socia—«спутницей трохоиды»), тождественную с полным оборотом синусоиды. Название «линия синусов» встречается впервые у французского иезуита Онорэ Фабри в сочинении «Геометрический труд о линии синусов и циклоиде», опубликованном им под псевдонимом А. Фарбиуса и вообще относящемся к предыстории исчисления бесконечно малых. Валлис в части II своей «Механики» (1670) правильно разобрал вопрос о знаках синуса во всех четырех квадрантах и вычертил два полных оборота синусоиды, отметив при этом, что их бесчисленно много. В другом месте он указал, что линия синусов служит границей развернутой на плоскость поверхности «цилиндрического копыта». Несколько позднее он нарисовал ветви линии секансов, но не заметил, что в вершинах они должны, быть направлены горизонтально, и соединил обе половины под прямым углом. Дж. Грегори в своих «Геометрических этюдах» (1668) представил часть тангенсоиды, лежащую в первом квадранте. Кривые секанса, тангенса и косинуса для первого квадранта были изображены на одном чертеже в «Геометрических лекциях» (Лондон, 1670, 2-е изд., 1674) И. Барроу. Однако линия секансов вычерчена там по крайней мере весьма неточно, а на других чертежах линия тангенсов даже просто неверна. Знаки тангенса в различных квадрантах впервые правильно установил, не приведя ни чертежа, ни доказательства, Ланьи. Котес в «Различных произведениях», приложенных к «Гармонии мер» (опубликовано в 1722), дал правильные графики тангенса и секанса для двух оборотов. Но еще Ф. Майер, обладавший вообще весьма серьезными заслугами в области тригонометрии, считал синус и тангенс тупого угла положительными, а косинус и котангенс отрицательными.

Большие успехи, достигнутые к этому времени в Англии, лишь постепенно укрепились на материке Европы. В Германии в XVII столетии не появилось ни одной сколько-нибудь значительной книги по тригонометрии, и неоднократно выходили только краткие изложения, предназначенные для землемеров и сообщавшие теоремы без доказательства; авторы некоторых даже не пользовались логарифмическими вычислениями. Из этих книг мы назовем только весьма употребительные «Таблицы универсальной математики» (Виттенберг, 1664) Эгидия Штрауха и «Пандору математических таблиц» (Франкфурт, 1684 и 1688) Грюнебергера, во введении к которым был дан обзор тригонометрических теорем. Aвтор «Ясной математики» (Нюрнберг, 1689, 1695 и 1711) Иоганн Штурм, кратко говоривший в ней и о тригонометрии, пропустил секансы как линии, без которых можно легко обойтись.

Несколько больше мы находим у французов. Прежде всего мы должны указать на известные уже нам большие энциклопедические работы Дешаля и Озанама. «Курс или мир математики» 1674, три тома; 1690, четыре тома) Дешаля заключал в первом томе полный обзор плоской и сферической тригонометрии, хотя еще в традиционной форме, с геометрическими доказательствами и без сокращенных обозначений. Задачу о вычислении двух углов β и γ по их сумме и отношению их синусов он рассматривал несколько иначе, чем Стрит. Он полагал

sin β: sin γ = tg j: tg ψ,

брал j произвольным и отсюда с помощью логарифмов определял ψ. Выведя (разумеется, в старинной форме) из вышеприведенной пропорции новую:

Введение бесконечных рядов побудило вновь заняться формулами для sin n_j и cos n_j, уже ранее известными для отдельных целочисленных значений п, и распространить их на случай произвольного п. Основание этим исследованиям было положено главным образом Виетом, который вывел такие формулы вплоть до n =10. Он, как и Бюрги (в одной неопубликованной рукописи), уже заметил закон образования коэффициентов. Хотя Оутред по существу не пошел дальше результатов Виета, но выражения, помещенные в конце первого издания его «Ключа к математике» 1631), вплоть до n = 5, уже значительно превосходили по алгебраической форме изложение Виета.

Последний результат Оутреда здесь имел вид:

B sin а)в — 5 B sin аK -f 5-2 sin а = 2 sin 5а.

Оутред здесь указывал, что радиус вообще можно положить равным 1; однако осуществил это лишь Эйлер. Во втором издании в 1648 Оутред дал соответствующую формулу для sin 7a. Он составил еще более обширный трактат о «сечениях угла» (опубликован в Opuscula math, hactenus inedita, Оксфорд, 1677). Там формула, соответствующая приведенной нами, гласила:

В своих работах Ланьи; которые были посвящены «гониометрии», введенной им в качестве новой науки об измерении всех углов. Первая была почти целиком посвящена одному чисто геометрическому методу, который состоял в том, что отношение между соответствующей углу дугой и полуокружностью представлялось в форме цепной дроби с помощью накладывания дуги на полуокружность, остатка — на дугу и т. д., продолжающегося, пока остаток не окажется уже неприметным. Другой, чисто аналитический прием был подробнее приведен преимущественно во второй статье. По существу он заключался в употреблении ряда для арктангенса. Но для уточнения вычислений Ланьи почти повсюду ввел замечательные усовершенствования. Так, например, он определял меньший острый угол прямоугольного треугольника со сторонами 3, 4, 5 с точностью до 1/60 ¹⁰ градуса. В третьей статье он привел выражение для общего члена ряда, получающегося из ряда арктангенса при сложении каждых двух последовательных его членов, и определил границы погрешности, если ряд обрывается на некотором определенном члене. В четвертой статье Ланьи указал, до каких пор следует продолжать вычисления при определении по его методу одного из острых углов прямоугольного треугольника по сторонам.

Немаловажные успехи были сделаны еще до Эйлера в XVIII столетии и в решении треугольников. В первую очередь все более приближалась к современной форма, хотя иногда еще пропорции выражались словесно. Пример был подан и здесь И. Ньютоном в его «Универсальной арифметике» 1707. Он занимается задачей о решении треугольника по основанию; сумме боковых сторон и углу при вершине. Ньютон проводит биссектрису угла устанавливает пропорцию

с: (a + b) = sin 1/2γ: sine

В проблемах XI и XII Ньютон задает три стороны, сам вводит строчные буквы, полагая, впрочем, АВ = а, АС=Ь и ВС = с, и словесно устанавливает пропорцию. Выводимые им дальше формулы для половинного угла и формула Герона для площади треугольника были хотя и не новы, но появились у него в привычной для нас форме.

В Германии в это время большое распространение получили сочинения Вольфа. Однако и в них еще не были использованы достижения англичан ни по содержанию, ни в отношении формы теорем. Следует только отметить вид, который сообщил Вольф правилу Непера для прямоугольного сферического треугольника. Во Франции после сочинений Дешаля и Озанама появилась довольно объемистая книга Депарсье «Новые курсы тригонометрии» (1741), которая содержала хорошие семизначные таблицы синусов, тангенсов и секансов, значения которых приводились с интервалом в одну минуту, и восьмизначные таблицы логарифмов синусов и тангенсов с интервалом 10 минут.

Наиболее выдающимся представителем тригонометрии до Эйлера был, однако, Ф. фон-Оппель. И он принадлежал к числу последователей Майера. В книге «Анализ треугольников» (1746) Оппель поставил целью аналитически развить всю плоскую и сферическую тригонометрию из немногих предложений, выведенных геометрическим путем. Свое намерение он, действительно, осуществил, хотя буквенное обозначение Майера весьма затрудняет чтение его книги. Наиболее важно, что оба так называемых уравнения Молльвейде приводились здесь в современной нам форме. Оппель вывел их посредством вычислений из геометрически доказанной теоремы тангенсов.

Оппель первый вполне систематически основал сферическую тригонометрию на рассмотрении рассеченного у верхнего ребра трехгранника, обе боковые грани которого накладывались на плоскость основания. С помощью такого чертежа он вывел теоремы синусов и косинусов, заметил, что из этих двух теорем можно вывести все прочие формулы, и показал, как с помощью дополнительного треугольника можно получить для каждой формулы взаимную с ней. Он вывел очень много таких формул, не интересуясь, однако, их приведением к логарифмическому виду, так что, например, аналогии Непера у него отсутствовали.

Поиск по сайту: