 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вариационный метод
Этот метод очень важен для химических задач, и основан на вариационном принципе.
Допустим теперь, что мы не знаем ни собственных значений, ни собственных функций уравнения (III.15), а только гамильтониан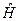 
. Возьмем некоторую произвольную нормированную функцию 
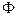и запишем равенство: 
Согласно условию (III.18) 
. Возьмем другую нормированную функцию 
и опять запишем равенство:
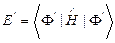, где 
. (III.19)
Если окажется, что 
, то это значит, что 
, то есть величина 
более близка к искомому значению 
. Следовательно, функция выбрана более удачно чем .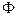
Иными словами мы должны подобрать пробную функцию 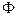так, чтобы интеграл 
был равен его наименьшему возможному значению для данной функции. Для этого надо, чтобы вариация интеграла 
по функции 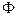обращалась в ноль, то есть, должно быть 
.
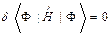Варьируя пробную функцию 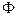, надо сохранять условие её нормировки, то есть, чтобы выполнялось требование 
. Это можно учесть в соответствии с методом Лагранжа, введя неопределенный множитель Лагранжа 
, и записав условие варьирования:
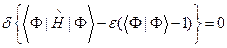(III.20)
Здесь стоит напомнить, что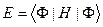 
зависит от вида функции 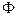, поэтому 
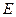является функцией от функции, т.е. функционалом. Поскольку мы хотим найти наименьшее значение энергии 
, эта задача состоит в поиске экстремума 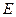. А исследование экстремальных значений функционалов проводится методами вариационного исчисления. Понятие “вариация” является обобщением понятия “дифференциал”. Обозначается символом 
и операции с вариациями можно проводить также как с обычными дифференциалами. Практически для того, чтобы удовлетворить условию (III.20), из каких-либо физических соображений подбирают пробную функцию 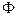как функцию некоторых параметров так, что её варьирование осуществляется с помощью варьирования этих параметров. Чем удачнее выбран вид 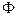и чем больше параметров, тем глубже получится минимум интеграла. Итак, уравнение (III.20) служит для нахождения приближения 
к наименьшему состоянию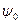 
. Интеграл 
определяет энергию 
, которая при должном выборе пробной функции 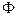имеет наиболее близкое к значение. В этом заключается суть этого метода.
Поиск по сайту: