Вариационный принцип

Если 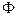– произвольная функция, удовлетворяющая условию , то выполняется соотношение , где – энергия основного состояния системы, то есть наименьшее собственное значение ее гамильтониана.

Для доказательства напишем уравнение Шредингера для нашей многоэлектронной системы:

(III.15)

Необходимо найти и 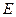. Мы знаем, что это уравнение имеет совокупность собственных значений , и – соответствующие собственные функции. Предположим, что мы знаем решение уравнения (III.15) и это есть нормированная функция 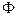. В силу свойства полноты набора собственных функций, 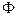может быть разложена в ряд по этим собственным функциям, то есть, представлена в виде

(III.16)

Здесь под “ ” подразумевается вся совокупность координат, характеризующих систему. Поскольку 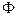описывает некоторое состояние системы, то средняя величина энергии в этом состоянии:

(III.17)

Заменим в (III.17) все значения 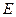наименьшим собственным значением . В результате это выражение или уменьшится или останется неизменным. Таким образом:

(III.18)

Очевидно знак равенства в (III.18) имеет место, когда 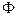совпадает с 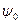, то есть является решением уравнения Шредингера, отвечающего минимуму полной энергии . Так что теорема доказана.

Поиск по сайту: