АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Дифференциальные уравнения порядка выше первого

Читайте также:
  1. II ОБЩИЕ НАЧАЛА ПУБЛИЧНО-ПРАВОВОГО ПОРЯДКА
  2. IV.1. Общие начала частной правозащиты и судебного порядка
  3. VI Дифференциальные уравнения
  4. Адаптивная полиномиальная модель первого порядка
  5. Алгебраические уравнения
  6. Анализ случаев нарушения безопасности движения с установлением виновных и конкретных нарушений правил и порядка работы
  7. Аналитическое выравнивание по параболе второго порядка
  8. Апериодическое звено второго порядка.
  9. Взаимосвязь правопорядка и функций государства
  10. Воб определении порядка пользования имуществом
  11. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  12. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.

Пусть n > 1. Как мы знаем, дифференциальное уравнение n-го порядка имеет вид

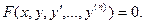(1)

 

Если уравнение (1) имеет вид

(1'),

то уравнение - го порядка (1') называется разрешенным относительно -ой производной. Функция 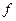в правой части уравнения (1') есть функция переменного. Общее решение уравнения (1') имеет вид

,

где 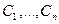– постоянные.

Общим интегралом уравнения (1) или (1') называется соотношение , задающее неявно решение уравнений (1) или (1'), соответственно.

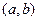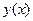Теорема 1. Пусть правая часть уравнения (1'), рассматриваемая как функция переменного , непрерывна, и имеет в некоторой окрестности точки непрерывные частные производные . Тогда на некотором интервале , содержащем точку , найдется раз непрерывно дифференцируемое решение уравнения (1'), удовлетворяющее условиям

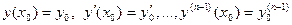. (2)

При этом решение дифференциального уравнения (1'), удовлетворяющее условиям (2), единственно.

Условия (2) называются начальными. Задача отыскания решения дифференциального уравнения (1'), удовлетворяющего начальным условиям, называется задачей Кoши.

9) Понижение порядка уравнения.

В процессе интегрирования уравнения - го порядка иногда удается получить уравнение более низкого порядка, эквивалентное исходному уравнению -го порядка в том смысле, что оба уравнения имеют одни и те же решения. Такие уравнения более низкого порядка называются промежуточными интегралами. Промежуточный интеграл порядка так же называют первым интегралом.

Пример 1. Дифференциальное уравнение второго порядка может быть записано как . Поэтому оно имеет первый интеграл .

Рассмотрим простейшие случаи, когда возможно понижение порядка дифференциального уравнения и, тем самым, сведение более сложной задачи к более простой.

I. Уравнение не содержит искомой функции и ее производных до порядка k-1 включительно, т.е. имеет вид следующий вид:

.

В этом случае порядок уравнения может быть понижен до подстановкой , так как в результате такой подстановки уравнение приобретает вид . В частности, если уравнение второго порядка не содержит , т.е. имеет вид , то подстановка приводит к уравнению первого порядка .

Пример 1. Решить уравнение .

Решение. Полагая , получаем , или , откуда p=C1x, т.е. . Интегрируя последовательно три раза, получаем:

 

, , .

 

Ответ:

II. Уравнение не содержит независимого переменного , т.е. имеет вид

. (1)

В этом случае порядок дифференциального уравнения можно понизить на 1, рассматривая как независимое переменное, как неизвестную функцию переменного и составляя дифференциальное уравнение для 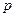. Например, пусть нам дано дифференциальное уравнение

(2)

Имеем 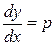, , откуда из (2) получаем дифференциальное уравнение для функции 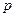переменного :

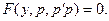
Если (1) есть уравнение третьего порядка

(3)

то, поскольку

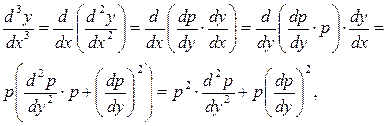
из (3) получаем дифференциальное уравнение для функции 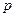переменного

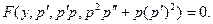
Пример 2. Решить уравнение

Решение. Непосредственно убеждаемся, что y=C есть решение. Далее считаем, что y не есть постоянная функция, и тем самым . Имеем или . Так как , то , или . Отсюда или . Разделяя переменные, получаем . Следовательно, , или , . Так как есть решение исходного уравнения, и y=C можно получить как , то общее решение дифференциального уравнения (4) есть

III. Левая часть уравнения является производной некоторой функции .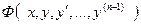

В этом случае порядок уравнения снижается на единицу, т.к. уравнение можно переписать в виде

, откуда .

Пример3. Решить уравнение

Решение. , поэтому . Это уравнение является линейным уравнением первого порядка. Находим его решение по методу Бернулли: , , . Интеграл от функции не выражается в элементарных функциях, поэтому пишем

 

, .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)