АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Линейное дифференциальное уравнение первого порядка

Читайте также:
  1. Адаптивная полиномиальная модель первого порядка
  2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  3. Апериодическое звено второго порядка.
  4. Билинейное Z – преобразование.
  5. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  6. Введение в анализ и дифференциальное исчисление
  7. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  8. Внутренняя энергия идеального газа. Работа газа при изобарном расширении. Применение первого начала термодинамики к изопроцессам. Понятие о втором начале термодинамики.
  9. Волна вероятности. Уравнение Шредингера
  10. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  11. Вопрос 4: Траектория движения. Криволинейное движение. Нормальное и тангенциальное ускорения при криволинейном движении.
  12. Вопрос: Основные пути укрепления законности и правопорядка.

Дифференциальное уравнение вида

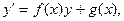
где 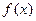и некоторые заданные функции, называется линейным

дифференциальным уравнением первого порядка.

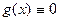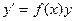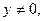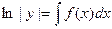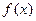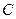Если , то уравнение имеет вид и называется однородным. Его решением является . Если то разделяя переменные, получаем откуда , или , где - примитивная функции . Следовательно, ненулевые решения однородного уравнения имеют вид , где – произвольная постоянная, отличная от нуля. Полагая , получим нулевое решение. 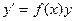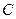Таким образом, все решения дифференциального уравнения могут быть найдены по формуле , где – произвольная постоянная, – примитивная функции .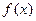

Для решения неоднородного линейного дифференциального уравнения применим метод Лагранжа вариации произвольной постоянной: в общем решении однородного уравнения заменим постоянную 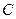функцией и будем искать решение неоднородного уравнения в виде . Имеем , откуда . Следовательно, в качестве можно взять любую примитивную функции . Пусть . Тогда общим решением линейного дифференциального уравнения будет функция


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

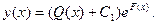
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)