 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примеры задач, приводящих к дифференциальным уравнениям
Основные понятия.
Дифференциальным уравнением называется уравнение, в которое неизвестная функция входит под знаком производной или дифференциала. Если искомая функция 
есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.
Мы будем рассматривать лишь обыкновенные дифференциальные уравнения.
Порядком дифференциального уравнения называется максимальный порядок входящей в уравнение производной (или дифференциала) неизвестной функции.
Решением дифференциального уравненияназывается функция, которая при подстановке в дифференциальное уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой. Отметим, что каждое решение имеет, вообще говоря, свой интервал, на котором оно задано.
Процесс нахождения решений дифференциального уравнения носит название интегрирования дифференциального уравнения.
Основная задача интегрального исчисления – отыскание функции , производная которой равна данной непрерывной функции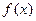 
(нахождение 
) – сводится к простейшему дифференциальному уравнению 
.
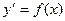Мы будем считать дифференциальное уравнение проинтегрированным, если задача отыскания его решения сведена к задаче одного из предшествующих разделов курса. Например, если найдено соотношение, определяющее решение как неявную функцию 
, или же выражено при помощи квадратур (интегралов).
Примеры задач, приводящих к дифференциальным уравнениям.
Пример 1. В инженерной практике часто бывает необходимо найти закон движения тела под влиянием заданных действующих сил. Движение считается прямолинейным.
По закону Ньютона сила равна произведению массы на ускорение. Поэтому
,
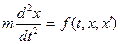где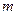 
– масса, – пройденный путь, 
– время,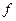 
– сила.
Пример 2. Радиоактивный распад.
Из эксперимента известно, что скорость распада радиоктивного вещества пропорциональна имеющемуся количеству вещества. Таким образом, если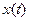 
– масса вещества, еще не распавшегося к моменту времени , то скорость распада удовлетворяет уравнению
где 
– некоторая положительная постоянная. В уравнении (1) перед поставлен знак -, так как 
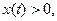а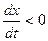 
.
Уравнение (1) называется дифференциальным уравнение радиоактивного распада.
Пример 3. Найти уравнение кривой на плоскости, обладающей тем свойством, что угловой коэффициент касательной в любой её точке равен удвоенной абсциссе.
Решение. Согласно условию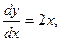 
откуда 
.
Поиск по сайту: