 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнения с раздельными и разделяющимися переменными
Дифференциальное уравнение вида

называется уравнением с разделенными переменными.
Дифференциальное уравнение вида
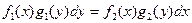 (2)
(2)
называется уравнением с разделяющимися переменными.
Путем деления на  , оно приводится к дифференциальному уравнению
, оно приводится к дифференциальному уравнению
 ,
,
которое имеет вид (1).
Будем считать в (1) 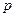 и
и 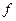 – непрерывными функциями, а
– непрерывными функциями, а  функцией независимого переменного
функцией независимого переменного  . Выражение
. Выражение 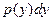 слева есть дифференциал некоторой функции
слева есть дифференциал некоторой функции 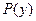 , зависящей от
, зависящей от  , а выражение
, а выражение  справа – дифференциал некоторой функции
справа – дифференциал некоторой функции  , зависящей от
, зависящей от  Решениями дифференциального равнения (1) будут те и только те дифференцируемые функции
Решениями дифференциального равнения (1) будут те и только те дифференцируемые функции  , которые при некоторой постоянной
, которые при некоторой постоянной 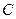 удовлетворяют уравнению
удовлетворяют уравнению 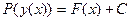 . При этом следует помнить, что если
. При этом следует помнить, что если 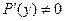 , то по теореме о неявной функции функция
, то по теореме о неявной функции функция  , определяемая неявно уравнением
, определяемая неявно уравнением 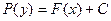 , где
, где 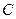 – произвольная постоянная, будет дифференцируемой.
– произвольная постоянная, будет дифференцируемой.
Пример 1. Решить дифференциальное уравнение
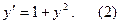
Решение. Разделим в (2) переменные и придем к уравнению
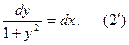
Решением дифференциального равнения (2) будет функция  такая, что
такая, что 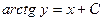 , где
, где 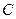 – произвольная постоянная. Отсюда
– произвольная постоянная. Отсюда  .
.
Пример 2. Решить дифференциальное уравнение
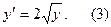
Решение. Очевидно, функция  есть решение уравнения (3). Пусть теперь y>0. Разделим в (3) переменные и придем к уравнению
есть решение уравнения (3). Пусть теперь y>0. Разделим в (3) переменные и придем к уравнению
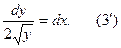
Проинтегрировав (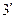 ), получим
), получим  где
где 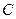 – произвольная постоянная. Отсюда следует, что
– произвольная постоянная. Отсюда следует, что  ,
,  . Таким образом, при каждом фиксированном значении
. Таким образом, при каждом фиксированном значении 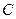 функция
функция  ,
,  является решением уравнения (3). Других решений это уравнение в полуплоскости
является решением уравнения (3). Других решений это уравнение в полуплоскости 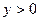 не имеет.
не имеет.
Пример 3. Проинтегрировать уравнение
 (4)
(4)
Решение. В этом уравнении переменная  не может принимать значение 0. Поэтому возможно деление на
не может принимать значение 0. Поэтому возможно деление на  . Разделив в (4) переменные, получим
. Разделив в (4) переменные, получим
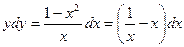 . (
. (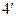 )
)
Проинтегрировав (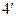 ), имеем
), имеем 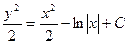 , или
, или 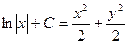 . Постоянную
. Постоянную 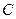 запишем в виде
запишем в виде  .Тогда
.Тогда 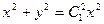 . Введем постоянную
. Введем постоянную  . Тогда общий интеграл уравнения (4) есть
. Тогда общий интеграл уравнения (4) есть
 .
.
В общем интеграле дифференциального уравнения первого порядка одна произвольная постоянная, которую принято обозначать как 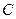 . По этой причине принято при переходе от одной произвольной постоянной к другой, например, от
. По этой причине принято при переходе от одной произвольной постоянной к другой, например, от 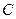 к
к  от
от  к
к  , индексы не записывать. Следовательно, общий интеграл уравнения (4) имеет вид
, индексы не записывать. Следовательно, общий интеграл уравнения (4) имеет вид
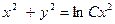 (С> 0).
(С> 0).
Пример 5. Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию.
 (5)
(5)
Решение. Мы ищем решение 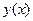 дифференциального уравнения (5) в окрестности точки
дифференциального уравнения (5) в окрестности точки 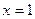 , удовлетворяющее условию
, удовлетворяющее условию  . Дифференцируемая функция
. Дифференцируемая функция
непрерывна. Поэтому окрестность точки 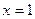 будем считать столь малой, что
будем считать столь малой, что
 (6)
(6)
для любого  из этой окрестности. Тогда
из этой окрестности. Тогда  . Разделив на
. Разделив на 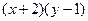 , получим
, получим  , откуда
, откуда

Следовательно, с учетом (6), общий интеграл данного уравнения есть
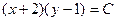 (С>0).
(С>0).
Найдем значение параметра 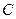 , которому соответствует кривая, удовлетворяющая начальному условию
, которому соответствует кривая, удовлетворяющая начальному условию  , то есть проходящая через точку (1,2)
, то есть проходящая через точку (1,2)  :
:
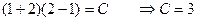
Таким образом, решением будет  такое, что
такое, что 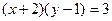 .
.
Пример 6. Проинтегрировать уравнение

Решение.
Разделив на  , получим
, получим
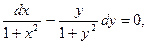
откуда
 , или
, или  .
.
Дифференциальное уравнение
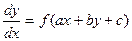
приводится к уравнению с разделяющимися переменными подстановкой 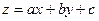 . Действительно,
. Действительно,  . Следовательно
. Следовательно
 , или
, или  откуда
откуда 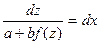 .
.
Дифференциальное уравнение
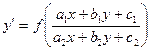
приводится к уравнению с разделяющимися переменными, если 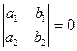 . Действительно, в этом случае
. Действительно, в этом случае 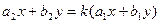 при некотором
при некотором  . Следовательно, дифференциальное уравнение может быть записано в виде
. Следовательно, дифференциальное уравнение может быть записано в виде
 ,
,
и по предыдущему подстановкой 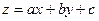 оно может быть приведено к уравнению с разделяющимися переменными.
оно может быть приведено к уравнению с разделяющимися переменными.
Поиск по сайту: