Гипербола

Определение. Гиперболой называется геометрическое место точек плоскости, разность расстояний от каждой из которых к двум фиксированным точкам плоскости, является величиной постоянной.

Основные характеристики гиперболы в основном аналогичные соответствующим характеристикам эллипса. Однако имеются различия. Гипербола фактически имеет только две вершины, а две другие вершины являются мнимыми. Соответственно различаются действительные и мнимые оси (полуоси). Между параметрами а, в и с для гиперболы имеет место соотношение:

в ²= а ²- с ².

Эксцентриситет Е для гиперболы всегда больше единицы. Гипербола также имеет две асимптоты. Каноническое уравнение гиперболы с центром симметрии в точке М (α; β) и действительной осью, расположенной на оси Ох, имеет вид:

.

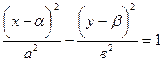Если центр симметрии поместить в точку О (0;0), то каноническое уравнение гиперболы примет вид:

.

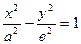Уравнения 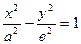и 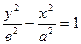определяют взаимно сопряженные гиперболы.

Задача. Найти основные характеристики и построить гиперболу, заданную уравнением: 4 х ²-9 у ²=36.

Решение:

Приведем уравнение гиперболы к каноническому виду.

.

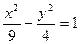Это уравнение определяет гиперболу, центр симметрии которой находится в точке О (0;0). Действительная ось гиперболы будет находится на оси Ох и равняется 2 а =6, а мнимая ось - на оси Оу. Она будет равна 2 в =4. Тогда вершинами гиперболы будут точки А (3;0), А ₁(-3;0). Мнимые вершины гиперболы будут в точках В (0;2) и В ₁(0)-2). Найдем фокусы гиперболы. Из соотношения в ²= а ²- с ², находим:

.

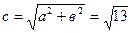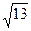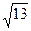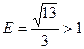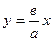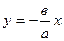Следовательно, фокусами гиперболы будут точки F ₁(;0) и F ₂(- ;0). Эксцентриситет гиперболы будет равен . Асимптоты гиперболы будут определяться уравнениями и или .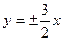

Построим гиперболу.

В

F ₁ А ₁ А F

Поиск по сайту: