 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Степенные ряды. Область сходимости степенных рядов
Функциональный ряд вида
(1)
или вида
, (2)
где коэффициенты Со, С 1, С 2,... - заданные числа, а х - переменная, называется степенным рядом.
Ряд (2) простой заменой у = х - а сводится к ряду (1). Поэтому в дальнейшем мы сформулируем основные понятия и утверждения для ряда (1).
В отличие от области сходимости произвольного функционального ряда, которая может оказаться множеством точек сколь угодно сложной структуры, область сходимости степенного ряда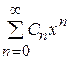 
всегда является промежутком оси х, который может быть отрезком, полуотрезком или интервалом, может вырождаться в одну точку х = 0 или совпадать со всей осью х.
Степенной ряд (1) всегда сходится в точке х = 0, т.к. при х = 0 он превращается в числовой ряд
.
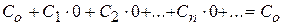Существуют степенные ряды, сходящиеся только в точке х = 0, например, ряд 
.
Действительно, применяя признак Даламбера, получаем для любого х ¹ 0:
.
Следовательно, данный ряд расходится при любом х ¹ 0.
Существуют степенные ряды, сходящиеся на всей оси х, например, ряд 
. По признаку Даламбера получаем для любого х ¹ 0:
.
Следовательно, данный ряд сходится на промежутке (-¥;¥).
Но, например, ряды
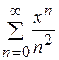(3)
сходятся на конечных промежутках (-1;1) и [-1;1] соответственно (проверить самостоятельно).
Норвежский математик Абель доказал следующее утверждение.
Теорема. Пусть дан степенной ряд 
. Если он сходится в некоторой точке х = хо ¹ 0, то он сходится, причем абсолютно, во всех точках х, удовлетворяющих неравенству |х|<|хо|; если он расходится в некоторой точке х = х1, то он расходится во всех точках, удовлетворяющих неравенству |х|>|х1|.
С геометрической точки зрения теорема Абеля утверждает следующее:
Если ряд сходится в точке хо, то он сходится абсолютно во всех точках, расположенных ближе к началу отсчета на числовой оси, чем хо, т.е. на интервале (-хо;хо). И если ряд расходится в точке х1, то он расходится во всех точках, расположенных дальше от начала отсчета на числовой оси, чем х1.
 |
- хо о хо х - х 1 о х 1 х
Таким образом, если степенной ряд 
сходится не только в точке х = 0 и не на всей числовой оси, то существует число R > 0 такое, что при всех х, для которых | х | < R степенной ряд сходится, а при всех х, для которых | х | > R, он расходится. Это число R называется радиусом сходимости, интервал (- R; R) - интервалом сходимости. Если степенной ряд сходится на всей числовой оси, то полагают R = ¥, если же только в точке х = 0, то полагают R = 0. На концах интервала сходимости степенной ряд может как сходиться, так и расходиться (см. ряды (3)).
Одним из способов определения R является применение признаков Даламбера или Коши абсолютной сходимости рядов. Покажем на примерах.
Примеры 41. Найти область сходимости следующих рядов:
а)  ,
| б)  ,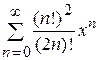
| в)  .
|
Решение.
а) Для данного ряда имеем:
.
Тогда по признаку Даламбера получаем:
.
Ряд сходится если D < 1, т.е., если | х | < 
.
Следовательно, 
, интервал сходимости 
.
Проверим сходимость ряда на концах интервала. При 
получаем:
Этот ряд расходится, т.к. 
. Аналогично при
х = - также получим расходящийся ряд, т.к. не выполняется необходимый признак сходимости.
Таким образом, областью сходимости данного ряда является интервал .
Замечание. Здесь можно было применить известную формулу Стирлинга
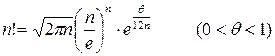(4)
или
.
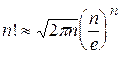Поэтому последовательность 
возрастающая, т.к.
при п ®¥.
Следует заметить, что формулу (4) впервые опубликовал в 1730 г. известный английский математик Джеймс Стирлинг (1692 – 1770 гг).
б) Применяем признак Даламбера
,
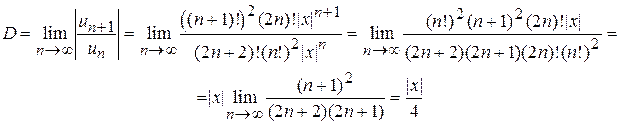Ряд сходится, если D < 1, т.е. 
или | x | < 4.
Следовательно, R = 4, интервал сходимости (-4;4). Проверим сходимость на концах интервала.
Если х = 4, то данный ряд примет вид:
.
Можно показать, что члены ряда образуют возрастающую последовательность (ап < ап+ 1, п = 1,2,...). Действительно, проверим выполнение неравенства:
, п = 1,2,...
Отсюда
, 
,
что требовалось показать.
Аналогично, показываем при х = -4.
Поэтому при х = ± 4 данный ряд расходится. Областью сходимости является интервал (-4;4).
в) Можно применить признак Даламбера, но мы используем признак Коши:
Ряд сходится, если С < 1, т.е. 
, или | х - 1| < 2. Отсюда получаем равносильные неравенства
- 2< x - 1 < 2 или - 1< x < 3.
Следовательно, R = 2 и интервал сходимости (-1;3). Проверим сходимость ряда в точках х = -1 и х = 3.
При х = 3 данный ряд примет вид:
.
Этот ряд сходится, как обобщенный гармонический при a = 2.
При х = -1 имеем:
.
Этот ряд абсолютно сходится, т.к. сходится ряд, составленный из абсолютных величин (см. теорему 1 § 3).
Таким образом, областью сходимости данного ряда является отрезок [-1;3].
Замечание. Если существует предел
или 
,
,
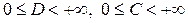то радиус сходимости степенного ряда 
, равен 
или 
. При этом при D = + ¥ или С = + ¥ полагают R = 0; при D = 0 или С = 0 считают R =+ ¥.
Следовательно,
. (5)
Этими формулами можно пользоваться, если все Сп ¹ 0.
1. Разложение функций в степенные ряды.
2. Ряды Тейлора и Маклорена.
Поиск по сайту: