Перейдем теперь к произвольным функциям

Пример 48. Разложим в ряд Маклорена следующие функции:

а)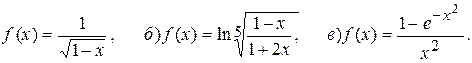

Решение.

а) Применяя биномиальный ряд 5:

,

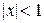при 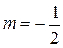и, заменяя х на - х, получаем:

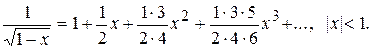
Итак,

.

б) Преобразуем данную функцию.

.

Применяем известный ряд 4:

.

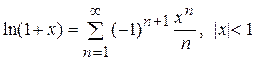Тогда получаем:

,

.

Следовательно,

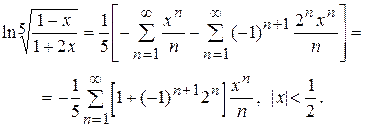
в) Известно, что показательная функция разлагается в ряд 1.

,

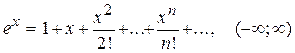поэтому

.

Следовательно,

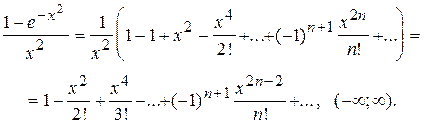
Заметим, что функция в точке х = 0 не определена, но имеет в этой точке предел:

.

Здесь мы воспользовались замечательным пределом для показательной функции

.

Таким образом, определив функцию f (х) в точке х = 0, полагая

f (0) = 1,

получим функцию

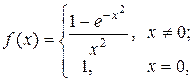
для которой справедливо полученное разложение для функции :

.

Поиск по сайту: