Решение систем линейных уравнений матричным способом

Пусть имеется система линейных уравнений:

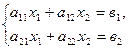
Введем матрицы: .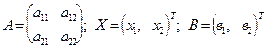

Тогда исходную систему линейных уравнений можно записать следующим образом: АХ = В; отсюда матричное решение будет иметь вид: Х = А^-1В.

Примечание. Матричным способом можно решать систему линейных уравнений лишь в том случае, когда матрица из коэффициентов при неизвестных будет обратимой.

П р и м е р. Решить матричным способом систему линейных уравнений: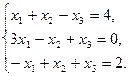

Решение:

находим определитель D:

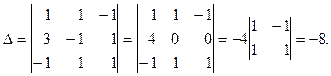
Поскольку D¹0, следовательно матрица из коэффициентов при неизвестных будет обратимой и, следовательно, систему линейных уравнений можно решить матричным способом.

.

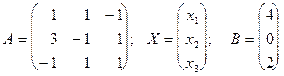Находим алгебраические дополнения элементов матрицы А.

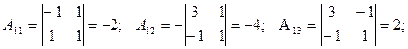
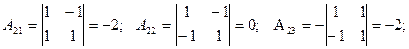
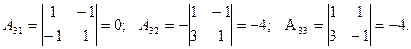
Найдем обратную матрицу А^-1:

.

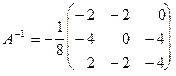Найдем решение системы линейных уравнений:

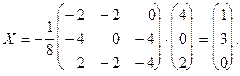
Таким образом, 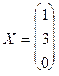. Поскольку матрица 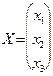, получим следующее решение: х₁ = 1; х₂ = 3; х₃ = 0.

Ответ: х₁ = 1; х₂ = 3; х₃ = 0.

Поиск по сайту: