 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задания для самостоятельной работы. Задание 1. По координатам вершин пирамиды А1А2А3А4 найти: 1) длины ребер А1А2 и А1А3; 2) векторы и в системе орт i
Задание 1. По координатам вершин пирамиды А1А2А3А4 найти: 1) длины ребер А1А2 и А1А3; 2) векторы 
и 
в системе орт i, j, k и их направляющие косинусы; 3) угол между векторами и ; 4) проекцию вектора на направление вектора 
; 5) угол между гранями А1А2А3 и А1А2А4; 6) площадь грани А2А3А4; 7) единичный нормальный вектор грани А1А3А4; 8) длину высоты пирамиды, опущенной из вершины А2 на грань А1А3А4.
Задание 2. Для векторов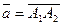 
и 
проверить равенство 
, определяя значение sin φ с помощью скалярного произведения векторов.
Примечание 1.
Для определенности заданий координаты вершин А1 (а1;в1;с1), А2 (а2;в2;с2), А3 (а3;в3;с3), А4 (а4;в4;с4) заданы соответственно столбцами матриц: 
.
№№ 3.2.1-3.2.20
3.2.1.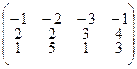 
3.2.2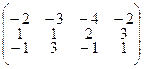 
3.2.3 
3.2.4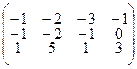 
3.2.5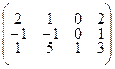 
3.2.6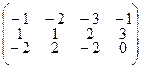 
3.2.7 
3.2.8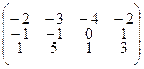 
3.2.9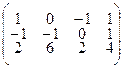 
3.2.10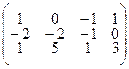 
3.2.11 
3.2.12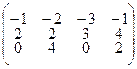 
3.2.13 
3.2.14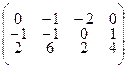 
3.2.15 
3.2.16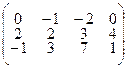 
3.2.17 
3.2.18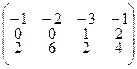 
3.2.19 
3.2.20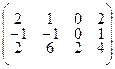 
Примечание 2. Задание 2 выполняется с использованием ЭВМ.
1. Уравнение прямой на плоскости.
2. Прямая линия на плоскости.
Поиск по сайту: