Ранг матрицы. Определение. Матрица А называется канонической, если все или несколько начальных элементов а11, а22,···акк

Определение. Матрица А называется канонической, если все или несколько начальных элементов а₁₁, а₂₂,··· а_кк, ее главной диагонали равны единице, а все остальные элементы матрицы равны нулю.

Любая матрица А может быть приведена к каноническому виду А_ч,с помощью элементарных преобразований: а) перестановки столбцов (строк); б) умножения строки (столбца) на число, отличное от нуля; в) прибавления к элементам любой строки (столбца), соответствующих элементов другой строки (столбца), умноженных на произвольное число.

В результате элементарных преобразований матрицы А будем получать матрицы, которые называются эквивалентными. Если матрица А_r эквивалентная матрице А, то это записывается следующим образом: А ~ А_r.

Определение. Рангом матрицы А называется наивысший порядок минора М_ij элементов а_{i j} этой матрицы, которой отличный от нуля.

Для определения ранга матрицы А =(а_ij) удобно преобразовать ее к каноническому виду. Тогда число единиц главной диагонали матрицы и будет выражать ее ранг.

П р и м е р. Найти ранг матрицы

.

Решение:

С помощью элементарных преобразований приведем матрицу А к каноническому виду.

~ ~

~ .

Ранг матрицы А будет равен двум.

Ответ: r_А =2.

2.1.1 2.1.2

2.1.3 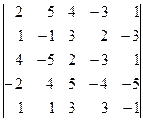2.1.4

2.1.5 2.1.6

2.1.7 2.1.8

2.1.9 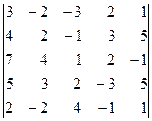2.1.10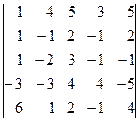

2.1.11 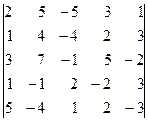2.1.12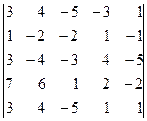

2.1.13 2.1.14

2.1.15 2.1.16

2.1.17 2.1.18

2.1.19 2.1.20

Поиск по сайту: