 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задания для самостоятельной работы. Вычислить пределы функций:
Вычислить пределы функций:
№6.1.1
1)  х0 =0; х0 =3;
х0 =0; х0 =3;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7) 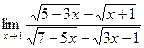 .
.
№6.1.2
1)  ; x0 =1; x0 =-1;
; x0 =1; x0 =-1;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№6.1.3
1)  х0 =1; х0 =2;
х0 =1; х0 =2;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  6)
6)  ;
;
7)  .
.
№6.1.4
1)  ; х0 =1; х0 =-2;
; х0 =1; х0 =-2;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.5
1)  ; х0 =0; х0 =3;
; х0 =0; х0 =3;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  6)
6)  ;
;
7)  .
.
№6.1.6
1)  ; x0 =0; x0 =1;
; x0 =0; x0 =1;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№6.1.7
1)  ; x0 =1; x0 =3;
; x0 =1; x0 =3;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.8.2
1)  ; x0 =1; x0 =-3;
; x0 =1; x0 =-3;  ; 2)
; 2)  ;
;
3)  4)
4)  ;
;
5)  ; 6)
; 6)  ;
;
7) 
 .
.
№ 6.1.9
1)  ; x0 =0; x0 =-2;
; x0 =0; x0 =-2;  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.10
1)  ; x0 =0; x0 =4;
; x0 =0; x0 =4;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.11
1)  ; x0 =0; x0 =5;
; x0 =0; x0 =5;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 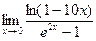 ;
;
7)  .
.
№ 6.1.12
1)  ; x0 =1; x0 =-4;
; x0 =1; x0 =-4;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.13
1)  ; x0 =1; x0 =-1;
; x0 =1; x0 =-1;  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.14
1) 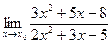 ; x0 =-1; x0 =1;
; x0 =-1; x0 =1;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.15
1)  ; x0 =0; x0 =-5;
; x0 =0; x0 =-5;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7) 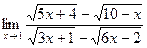 .
.
№ 6.1.16
1)  ; x0 =0; x0 =-2;
; x0 =0; x0 =-2;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.17
1)  ; x0 =0; x0 =5;
; x0 =0; x0 =5;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.18
1) 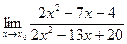 ; x0 =1; x0 =4;
; x0 =1; x0 =4;  ; 2)
; 2) 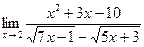 ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
№ 6.1.20
1)  ; x0 =1; x0 =-3;
; x0 =1; x0 =-3;  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  .
.
Примечания.
1) Вычисление пределов не предполагает использования правила Лопиталя;
2) Предел №7 каждого задания следует вычислять с использованием ЭВМ;
3) При вычислении пределов следует иметь в виду, что при  выполняется условие: x~sinx ~ arcsinx ~ arctgx ~ ln(1+x) ~(ex-1). Все эти функции будут эквивалентными, бесконечно малыми, непрерывными функциями.
выполняется условие: x~sinx ~ arcsinx ~ arctgx ~ ln(1+x) ~(ex-1). Все эти функции будут эквивалентными, бесконечно малыми, непрерывными функциями.
1. Непрерывность функции.
- Точки разрыва и их классификация.
Определение. Функция называется непрерывной в точке  , если выполняется условие:
, если выполняется условие: 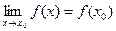 .
.
Обычно при исследовании функции на непрерывность в точке  вычисляют односторонние пределы, т.е. в определение
вычисляют односторонние пределы, т.е. в определение 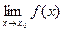 добавляются условия х < x 0 и x > x 0. Это символически записывается следующим образом:
добавляются условия х < x 0 и x > x 0. Это символически записывается следующим образом:
 ;
;  .
.
П р и м е р. Исследовать функцию на непрерывность. Сделать чертеж.
 .
.
Решение:
1) Находим односторонние пределы в точке х = -1. Найдем левосторонний предел:  . Найдем правосторонний предел в точке х =-1:
. Найдем правосторонний предел в точке х =-1:  . Поскольку односторонние пределы равны и они равны значению функции в точке х = -1, то в этой точке функция будет непрерывной.
. Поскольку односторонние пределы равны и они равны значению функции в точке х = -1, то в этой точке функция будет непрерывной.
2) Находим односторонние пределы функции в точке х =1.  ;
;  . Поскольку
. Поскольку  , функция в точке х =1 будет иметь разрыв. Так как односторонние пределы конечны, то разрыв функции в точке х=1 будет разрывом первого рода. В точке х =1 функция имеет скачок
, функция в точке х =1 будет иметь разрыв. Так как односторонние пределы конечны, то разрыв функции в точке х=1 будет разрывом первого рода. В точке х =1 функция имеет скачок  . Схематический чертеж.
. Схематический чертеж.

Поиск по сайту: