АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Векторного произведения

Читайте также:
  1. Алгебраические свойства векторного произведения
  2. Алгоритм вычисления произведения
  3. Белорусское искусство XVIII века. График Гершка Лейбович, резчик Ян Шмитт, художники Хеские. Слуцкие пояса и другие произведения декоративно-прикладного искусства данной эпохи.
  4. В хороших литературных произведениях особое значение придается реакциям.
  5. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).
  6. Вопрос 8. Герои романтических поэм А. С. Пушкина (на примере одного произведения).
  7. Вопрос35. Предел Функции в точке и на бесконечности. Геометрическая иллюстрация определений. Предел постоянной. Предел суммы, частного, произведения. Предел элементарных функций.
  8. Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
  9. Глава девятая. Евангельский гуманизм в произведениях русских художников
  10. Для векторного произведения можно написать формулу, аналогичную (4).
  11. Драма Шиллера «Вильгельм Телль». Реализм и народность произведения.

Задача 1. Найти площадь Δ АВС, заданного координатами его вершин: А (2;1;-1), В (1;-1;2), С (0;-1;3).

Решение:

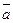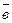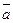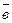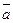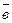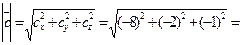
Образуем векторы . Найдем координаты векторов и : (-1;-2;3), (-2;0;4). Найдем векторное произведение векторов и : . Найдем модуль вектора :

. Модуль вектора будет выражать площадь параллелограмма, построенного на векторах 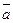и 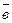. Поэтому площадь ΔАВС будет равна: .

Ответ: (ед2).

Задача 2. Используя условие задачи 1, найти единичный вектор нормали к плоскости, в которой лежит Δ АВС.

Решение:

Искомый вектор нормали будет коллинеарный вектору . Поэтому единичный вектор нормали к плоскости, определяемой Δ АВС, будет равен:

.

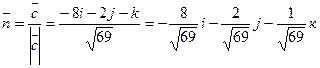Ответ: .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)