Свойства определителей

Раздел 1.

Линейная алгебра

План

1. Матрицы, действия над матрицами.

2. Определители и их свойства.

3. Невырожденные матрицы.

4. Обратная матрица.

1. Ранг матрицы.

1. Матрицы, действия над матрицами.

Определение. Матрицей размера m´n называется прямоугольная таблица произвольных элементов а_ij, которая содержит m строк и n столбцов и обозначается следующим образом: А =(а_ij)=|| а_i ||.

П р и м е р. - матрица размера 2´3, элементами которой являются числа.

Если m = n, то матрица в этом случае называется квадратной. Элементы а₁₁; а₂₂, ···, а_mn образуют главную диагональ матрицы. Квадратная матрица, в которой все элементы, кроме элементов главной диагонали, равны нулю называется диагональной.

Определение. Единичной называется диагональная матрица, в которой все элементы главной диагонали будут равны единице. Единичную матрицу принято обозначать буквой Е.

п р и м е р. - единичная матрица.

Матрица размера 1´ n называется матрицей-строкой, а матрица, размера m ´1 называется матрицей-столбцом.

Квадратная матрица А =(а_ij) имеет числовую характеристику, которой является определитель , составленный из элементов этой матрицы.

Примечание. Матрица - это таблица элементов (чисел), а определитель - это выражение, составленной из элементов и в случае, если элементы будут числами, определитель, в конечном итоге будет выражаться некоторым числом.

Действия с матрицами

1. сумма матриц

Матрицы А =(а_ij) и В =(в_ij) можно складывать в том случае, если они будут иметь одинаковый размер.

Определение. Суммой двух матриц А и В одинакового размера m ´ n называется матрица С = А+В, элементы которой определяются следующим образом: С_ij=а_ij + в_ij, т.е. С =|| а_ij + в_ij ||.

П р и м е р. , . Тогда .

2. Определители и их свойства.

Определение. Определителем второго порядка называется квадратная таблица некоторых элементов , которой в соответствие однозначно ставиться выражение (ad - вс).

Если а, в, с и d - произвольные числа, то определитель в конечном итоге будет выражаться также числом. Для однозначного определения местоположения элементов определителя вводится их двойная индексация. В общем виде элемент определителя, который стоит на пересечении i -ой строки и j -го столбца будет выражаться как a_ij.

Обозначается определитель символом D или , т.е. - символическое выражение определителя в общем виде.

- вычислительная схема определителя второго порядка в общем виде.

П р и м е р. Вычислить определитель .

Решение:

а ₁₁=6, а ₁₂=1, а₂₁=-5, а ₂₂=-2.

=6(-2)-(-5)1=-7.

Ответ: -7.

Определение. Определителем третьего порядка называется квадратная таблица некоторых элементов вида

,

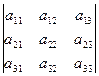которой в соответствие однозначно ставится выражение .

П р и м е р. Используя определение, вычислить определитель третьего порядка .

Решение:

В данном примере числовые значения элементов следующие: а ₁₁=1; а ₁₂=1; а ₁₃=-1; а ₂₁=2; а ₂₂=1; а ₂₃=-2; а ₃₁=-1; а ₃₂=1; а ₃₃=2. Подставляя эти значения в выражение определителя через его элементы, получим:

D=1×1×2+1×(-2)×(-1)+2×1×(-1)-(-1)×1×(-1)-2×1×2-1×(-2)×1=2+2-2-1-4+2=

=-1.

Определение. Минором М_ij элемента а_ij в определителе D, называется определитель, который получим после вычеркивания i -ой строки и j -го столбца в определителе D.

П р и м е р. Найти все миноры определителя .

Решение:

М ₁₁=1 (вычеркиваем первую строку и первый столбец). Аналогично М ₁₂=-3, М ₂₁=2, М ₂₂=6.

П р и м е р. Найти миноры М ₁₁; М ₂₁; М ₃₂ и М ₁₃ в определителе .

Решение:

.

Таким образом, если минорами определителя второго порядка являлись его элементы, то в случае определителя третьего порядка минорами являются определители второго порядка.

Определение. Алгебраическим дополнением элемента а_ij в определителе D, называется минор этого элемента М_ij, взятый с соответствующим знаком, который определяется следующим образом: А _ij = (-1 ^i+j) ^ijМ_ij.

Другими словами, если сумма номеров строки и столбца, на пересечении которых находится элемент а_ij определителя D будет четной, то алгебраическое дополнение будет совпадать с минором этого элемента. В противном случае алгебраическое дополнение и минор элемента а_ij будут отличаться знаком.

П р и м е р. Найти все алгебраические дополнения элементов определителя .

Решение:

А ₁₁= М ₁₁=-5; А ₁₂=- М ₁₂=1; А ₂₁=- М ₂₁=-4; А ₂₂= М ₂₂=2.

П р и м е р. Найти алгебраические дополнения элементов первой строки определителя и первого столбца: .

Решение:

Ответ: А ₄=-2; А ₁₂=-1; А ₁₃=3; А ₂₁=3; А ₃₁=4.

Свойства определителей

1. Если в определителе строки и столбцы поменять местами, то определитель при этой операции, которая называется транспонированием, не изменится.

2. Если в определителе поменять местами любые две строки, то абсолютная величина определителя не изменится, а знак изменится на противоположный.

3. Если в определителе имеются две одинаковые строки, то определитель равен нулю.

4. Общий множитель элементов строки можно выносить за знак определителя.

Следствие. Определитель в котором имеются пропорциональные строки равен нулю.

5. Сумма произведений элементов строки на их алгебраические дополнения равна величине определителя. Эту операцию называют разложением определителя по элементам строки.

6. Сумма произведений элементов строки на алгебраические дополнения элементов параллельной строки определителя равна нулю.

7. Определитель не изменится если к элементам любой строки прибавить элементы параллельной строки, умноженные на произвольное число.

В практическом отношении наиболее важными являются первое, пятое и седьмое свойства. Так, с учетом первого свойства, строки и столбцы определителя являются равноправными, т.е. все приведенные свойства относительно элементов строк определителя выполняются и для элементов столбцов. Пятое свойство вообще иногда приводится как определение определителя, с использованием этого свойства вычисление определителя третьего порядка сводится к вычислению трех определителей второго порядка, т.е. это свойство позволяет определители более высоких порядков вычислять с помощью определителей, порядок которых на единицу ниже. Наконец, седьмое свойство позволяет определитель преобразовать так, чтобы все элементы определенной строки, кроме одного, были нулевыми и затем вычислить определитель с использованием пятого свойства.

П р и м е р. Вычислить определитель 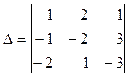с использованием различных его свойств.

Решение:

1. Вычислим определитель D, используя его определение:

D=1×(-2)×(-3)+2×3×(-2)+1×(-1)×1-(-2)×(-2)×1-(-1)×2×(-3)-1×3×1=-20.

2. Вычислим определитель, разложив его по элементам первой строки:

D= а₁₁А₁₁ + а₁₂А₁₂ + а₁₃А₁₃;

;

3. вычислим определитель, разложив его по элементам второго столбца.:

D= а₁₂А₁₂ + ₂₂А₂₂ + а₃₂А₃₂;

4. Вычислим определитель D, предварительно преобразовав его с использованием седьмого свойства.

.

К определителю , который мы получили, заменив в исходном определителе вторую строку суммой элементов первой и второй строки, применим пятое свойство, раскладывая его по элементам второй строки.

.

Ответ: D=-20.

Поиск по сайту: