АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные свойства пределов функций

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  3. I.3. Основные этапы исторического развития римского права
  4. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  5. II. Основные задачи и функции
  6. II. Основные показатели деятельности лечебно-профилактических учреждений
  7. II. Основные проблемы, вызовы и риски. SWOT-анализ Республики Карелия
  8. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  9. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  10. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  11. VI.3. Наследственное право: основные институты
  12. А) возникновение и основные черты

Пусть для функций f(x) и g(x) существуют пределы 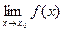и 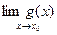и пусть С - произвольная постоянная. Тогда имеют место следующие соотношения:

1) ;

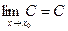2) ;

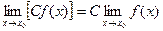3) ;

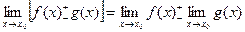4) ;

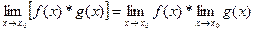5) 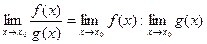, если .

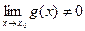Функция f(x) называется бесконечно малой при 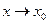, если 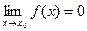. Функция F(x) называется бесконечно большой при 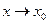, если .

Функции f(x) и g(x) называются эквивалентными, если выполняется одно из условий:

1) ; ;

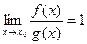2) ; .

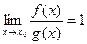В этом случае пишут: 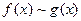. Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если эти функции заменить им эквивалентными.

 

 

Замечательные пределы.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)