АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Расширенная матрица данной системы имеет вид

Читайте также:
  1. I. Формирование системы военной психологии в России.
  2. II. Цель и задачи государственной политики в области развития инновационной системы
  3. II. Экономические институты и системы
  4. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  5. IV. Современные методы синтеза неорганических материалов с заданной структурой
  6. SWOT- матрица
  7. А). Системы разомкнутые, замкнутые и комбинированные.
  8. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство
  9. Абиотические компоненты экосистемы.
  10. Абстрактные линейные системы
  11. Автоматизированные системы контроля за исполнением документов
  12. Автоматизированные системы контроля и учета электроэнергии (АСКУЭ).

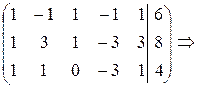
Выполним прямой ход метода Гаусса.

Умножим первую строку на (-1) и прибавим ко второй и третьей строке. Получим

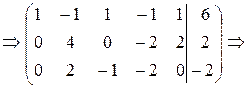
Меняем местами вторую и третью строки матрицы. Получаем

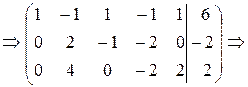
Вторую строку умножаем на (-2) и прибавляем к третьей. Получаем

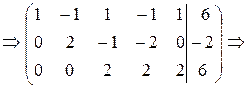
Разделим третью строку на 2. Получим

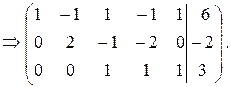
Итак, прямой ход осуществлен, в результате преобразования матрицы получим систему уравнений, эквивалентную заданной

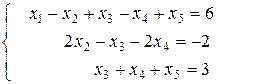
Обратный ход позволяет последовательно определить все неизвестные системы. Так как система содержит 5 неизвестных и всего 3 уравнения, то выберем x4, x5 - свободными переменными, а x1, x2 x3 – базисными переменными.

Из последнего уравнения находим x3=3-x4-x5 и подставляем во второе уравнение для определения x2. Получаем

Подставляем найденные x2 и x3 в первое уравнение и находим x1=6+x2-x3+x4-x5 = 6+ 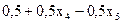-3+x4 +x5 +x4-x5;

x1=3,5+2,5x4-0,5x5.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)