Сделать чертеж

Решение:

1) Если ребро АВ обозначить за вектор 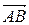, то длина ребра - это длина вектора. Находим координаты вектора :

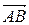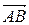=(- 2-10; 8-6; 2-6)=(- 12; 2;- 4).

Если 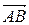=(х; у: z), то его длина .

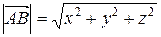Следовательно,

.

2) Угол между ребрами АВ и АD – это угол между векторам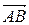и и 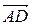. Находим координаты вектора .

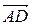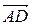=(7-10; 10-6;3-6)=(-3;4;-3).

Из пункта 1) нам известны координаты вектора 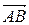=(- 12; 2;- 4). Угол между двумя векторами находится по формуле:

.

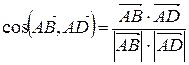Если векторы 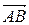и 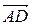имеют координаты 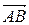=(х₁; у₁: z₁), 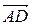(х₂; у₂: z₂) соответственно, то эта формула перепишется в виде:

.

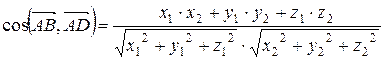Следовательно, получаем

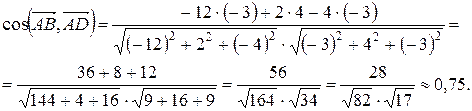
Итак, .

3) Уравнение прямой, проходящей через две точки М₁(х₁; у₁; z₁) и М₂(х₂; у₂; z₂) имеет вид:

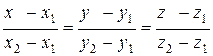
или равносильное ему уравнение:

,

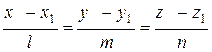где =(l,m,n) – координаты направляющего вектора прямой М₁М₂.

Направляющий вектор прямой – это вектор, параллельный прямой. В нашем случае прямая проходит через точки А(10; 6; 6) и В(- 2; 8; 2).Следовательно, уравнение прямой АВ:

.

Итак, каноническое уравнение прямой АВ:

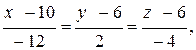
где направляющий вектор

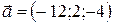
4) Уравнение плоскости по трем точкам находится по формуле:

, (*)

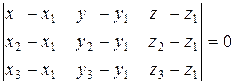где А(х₁; у₁; z₁); В (х₂; у₂; z₂); С(х₃; у₃; z₃) – точки, через которые проходит плоскость. Подставляя координаты точек А, В, С в формулу (*), получим:

.

Считаем определитель, разложив его по первой строке.

D=а₁₁А₁₁+а₁₂А₁₂+а₁₃А₁₃,

где - алгебраические дополнения элементов 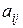, а М_{i j} – минор элемента 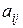. Минором элемента матрицы называется определитель, получаемый (вычеркиванием строки и столбца, на пересечении которых он расположен) из данного. Следовательно,

.

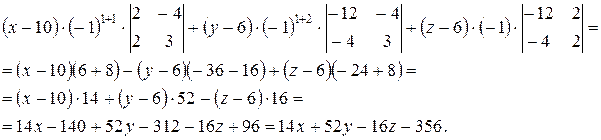
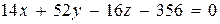Итак, уравнение плоскости АВС:

.

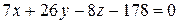Пример 5. Дана система линейных уравнений:

доказать ее совместность и решить тремя способами:

1) Методом Гаусса;

2) По формулам Крамера;

Поиск по сайту: