некоторые примеры применения производной в алгебре, геометрии и физике

Задача 1. Найти сумму 1+2*1/3+3(1/3)²+…+100(1/3)⁹⁹;

Решение.

Найду сумму g(x)=1+2x+3x²+…+100x⁹⁹ и подставлю в нее x=1/3.

Для этого потребуется вспомогательная функция f(x)=x+x²+…+x¹⁰⁰.

Ясно, что f ’(x)=g(x).

f(x) — сумма геометрической прогрессии.

Легко подсчитать, что f(x)=(x—x¹⁰¹)/(1—x). Значит,

g(x) = f ’(x) = ((1—101x¹⁰⁰)(1—x)—(x—x¹⁰⁰)(-1))/(1—x)²=(1—102x¹⁰⁰+101x¹⁰¹)(1—x)².

Подставлю x = 1/3.

Ответ: 0,25(9—205*3^-99)

Задача 2. Найти сумму 1+2*3+3*3²+…+100*3⁹⁹;

Решение.

Найду сумму g(x)=1+2x+3x²+…+100x⁹⁹ и подставлю в нее x=1/3.

Для этого потребуется вспомогательная функция f(x)=x+x²+…+x¹⁰⁰.

Ясно, что f ’(x)=g(x).

f(x) — сумма геометрической прогрессии.

Легко подсчитать, что f(x)=(x—x¹⁰¹)/(1—x). Значит,

g(x) = f ’(x) = ((1—101x¹⁰⁰)(1—x)—(x—x¹⁰⁰)(-1))/(1—x)²=(1—102x¹⁰⁰+101x¹⁰¹)(1—x)².

Подставлю x = 3.

Ответ: ≈ 2,078176333426855507665737416578*10⁵⁰.

Задача 3. Найдите площадь треугольника AMB, если A и B — точки пересечения с осью OX касательных, проведенных к графику y = (9—x²)/6 из точки M(4;3).

Решение.

т. A = у_кас1∩OX Решение:

т. B = у_кас2∩OX у_кас =y(x₀)+у’(x₀)(x—x₀);

y = (9—x²)/6 y’(x₀) = -2x*1/6 = -x/3;

M(4;3)________ т.к. у_кас проходит через M(4;3), то

S_AMB —? 3 = (9—x₀²) — (4—x₀)* x₀/3 | *3

18 = 9—x₀²—2x₀(4—x₀);

x₀²—8 x₀—9 = 0;

Д/4 = 16 + 9;

x₀ = 4+5 = 9;

x₀ = 4—5 = -1

у_кас1 = -12 — (x—9)*9/3 = -3x+15;

у_кас1 = 4/3 + (x+1)*1/3 = x/3+5/3;

A(5;0); B (-5;0);

AM = √10 (ед.);

AB = 10 (ед.);

BM = 3√10 (ед.);

p — по лу периметр; __

p = (4√10 + 10)/2 = 2√10 + 5;

__ __ __ __ __ __

S = √ (2√ 10 + 5 ) (2 √10 + 5—√ 10) (2√ 10 + 5—3√10) (2√10 + 5—10) =

= √ (2√10 + 5)(√10 + 5)(5—3√10)(2√10—5) =

= √(40—25)(25—10) = 15 (ед²);

Ответ: 15 (ед²).

Задача 4. Какая наименьшая плоскость может быть у треугольника OAB, если его стороны OA и OB лежат на графике функции y = (|x|—x)/2, а прямая AB проходит через точку M(0;1).

Решение:

-x, x<0

y =

0, x>0

A(a;-a); B (b;0);_

AO = |a|√2 = -a√2 (т.к. a<0);

BO = b;

Для т. B:

у₁ = kx +z;

т.к. у₁ —график линейной пропорциональности, проходящий через т M(0;1), то z = 1.

0=kx+1;

k=-1/b;

Для т. A:

у₁=kx+1;

-a=kx+1;

k=(-1-1a)/a;

у_1A= у_1B

(-a—a)/a = -1/b;

b+ab=a;

a(1—b)=b;

a = b/(1-b);

S_∆AOB=0,5*AO*OB*sin /_ AOB

ÐAOB =180^o — 45^o = 13 5 ^o

S_∆AOB=0,5*(√2/2)* (-a)b√2 = -ab/2;

S_∆AOB = -b²/(2(1—b)) = b²/(2(1—b)); D(y): b>1(т.к. при b<1 не образует ∆AOB.);

т.к. функция непрерывна и дифференцируема на b>1, то найду ее производную:

S’ = (4b(b—1)—b²)/(4(b—1)²) = (4b²—4b—2b²)/(4(b—1)²) = 2b(b—2)/(4(b—1)²) =

= b(b—2)/(2(b—1)²);

S’ = 0;

точки экстремума:

b=0;

b=1;

b=2;

но b>1, значит

S_наим = S(2) = 4/(2(2—1))=2(ед²);

Ответ: 2 ед².

Задача 5. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ с ребрами CD = 24, AD= 6 и DD₁ =4 проведена плоскость через центр симметрии грани A₁B₁C₁D₁, вершину А и точку Р, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью? На какие части делит точка P ребро DC в этом случае?

Решение. Проведем плоскость и построим сечение (рис.). АО Î АA₁C₁С - линия, принадлежащая данной плоскости. Продолжим АО до пересечения с CC₁ в точке S. Тогда SP - линия пересечения грани DD₁C₁C и данной плоскости, а сечение ANMP - параллелограмм. S_сеч = S_AMNP = SK*AP/2, потому что SK/2— высота параллелограмма ANMP. Это видно из следующего рассуждения.

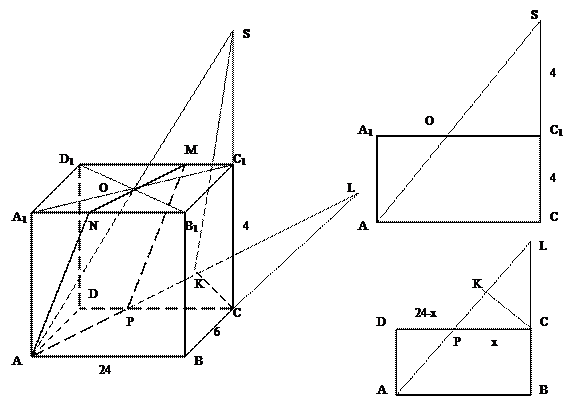В ΔASC ОC₁ - средняя линия (значит SC₁ = 4), в ΔPSC также средняя линия МC₁, а плоскость A₁B₁C₁D₁ делит пополам любую линию между S и плоскостью ABCD, а значит и SK.

Пусть PC = x; ΔCLP подобен ΔD AP,

LC/AD = x/(24—x), LC = 6x/(24— x); _____________ ____________

Из ΔCLP: KC = (6x*x/(24—x))/(√(36x²/(24—x)²)+x²) = 6x/(√(36+ (24—x)²);

________ ________ ___________ __________________

Из ΔSCK: SK = √ SC²+ KC² = √64+36x²/(36+(24—x)²) = 2√16+9x²/(36+(24—x)²);

Из ΔADP: AP = √36+(24 —x)²; _____ _________________ __________________

S_сеч = AP*SK/2 = 0,5*(√36+(24—x)²) 2√16+9x²/(36+(24—x)²) = √16(36+(24—x)²)+9x²;

Если S’(x) = 0, то 18x+16*2(24—x)(-1) = 0;

50x—32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min);

S_сеч = 312;

DP = 24—16*24/25 = 216/25;

Ответ: 312 кв. ед.; DC: 384/25; 216/25.

Задача 6. Высота пирамиды TABC с основанием ABC проходит через середину ребра AC. Выберите на AC точку М так, чтобы площадь сечения пирамиды плоскостью, проходящей через точку M, середину ребра TC и вершину B, была наименьшей, если AB=BC=AC=TC=2.

Решение. HF=FC=1/2;

S_∆BME = BM*EK*1/2; ___ _

Из ∆TCH => T H = √4—1=√3;

EF = TH/2=√3/2;

Пусть MC = x.

Из ∆BM C по тео реме косинусов MB²= x²+4—2*2*x*1/2;

MB = √x²—2x+4; _ _

S_∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2;

S_∆BMC = 0,5*BM*PC, _ ________

PC = (2S_∆BMC)/BM, PC = x√3/√x²—2x+4;

∆KMF подобен ∆PMC (по двум уг л ам):

KF/PC = MF/MC(рис 2), _____ _ _________

KF = x√3(x—1/2)/(x√x²—2x+4) = √3(x—1/2)/(√x²—2x+4);

________ ______________________

Из ∆KEF => KE = √ K F² +EF² = √3(x—1/2)²/(x²—2 x+4)+ 3/4; _

S_∆BME = 0,5√x²—2x+4 *√3(x—1/2)²/(x²—2x+4)+3/4 = 0,5√3(x—1/2)²+(x²—2x+4)*3/4;

Если S’(x) = 0, то

6(x—1/2)+(2x—2)*3/4 = 0;

15x—9 = 0;

x = 3/5; __

S(3/5) = √15 /5 кв.ед.

Ответ: √15/5 кв.ед.

Задача 7. В сферу радиусом R вписана правильная треугольная пирамида, у которой боковое ребро образует с высотой пирамиды угол 60^o. Какую наименьшую площадь может иметь треугольник MBK, если точка M лежит на апофеме пирамиды, а BK —высота основания пирамиды, не пересекающая апофему?

Решение. TP = 2R, ÐATO = 60^o.

Пусть AB = BC= CA = a(рис.)

Тогда AO = a√ 3 /3,

AD = BK = a√3/2, _ _

TO = AO * ctg60^o= a√3/3*1/√3 = a/3,

OD = a√3 /6,

AO² = TO*OP = TO(2R - TO),

a²/3 = a(2R – a/3)/3, a = 3R/2.

S_∆MBK = BK*LM*1/2, BK = const,

S_∆MBK = f(LM), __

LM = √MN²+NL²

Пусть MD = x, тогда MN = x cos / NM D; _

cos Ð NM D = TO/TD = a/(3√a²/9+a²/12 = 2/√7, MN = 2x/√7.

Из ∆ONL: LN = ON cos30^o (ÐONL = 30^o);

ON = OD – ND, _ _ _ _ _

ND = x s in ÐNM D =x √3/√7, ON = a√3/ 6 - x√3/√7,

LN = (a √3/6 - x√3/7)√3/2 = (a /4 – 3x/(2√7)),

LM = √4x²/7+(a/4 – 3x/(2√7))². _ _

Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0,

8x/7 – 3a/4√7 + 9x/14 = 0,

25x/14 = 3a /4 √7,

x = 21a/50√7. __ __

MN = (21a/50√7 )* (2/√7) = 3 a /25,

LN = a/ 4 – (3/2√7)*(21a/ 50√7 ) = 4a/25,

LM = √a²/6 2 5 + 9a²/625 = a √ 10/25. _

S_∆MBK = a √ 3/2*a/5*1/2 = a√3/20 = 9√3 R²/80.

Ответ: 9√3 R²/80.

Задача 8. В сферу радиусом R вписана правильная треугольная пирамида, высота которой в 1,5 раза меньше высоты основания. Между боковой гранью пирамиды и сферой расположена правильная четырехугольная призма, одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем.

Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу радиусом R,

SO*1,5 = AD,

LMN – правильная четырехугольная призма.

Найти. V_пр = f(LM).

Пусть SO = H, тогда AD = 1,5H;

SO₁ = R – радиус сферы; LM = x –высота призмы.

∆SKO₁ подобен ∆SOD => O₁K/OD = SO₁/SD => OK₁ = OD*SO₁/SD.

Из ∆AO₁O: R² = AO² + O₁O² = (2AD/3)² + (AD*2/3 - R)²,

R² = 4AD²/9 + 4AD²/9 –AD*R*4/3,

8AD²/9 = AD*R*4/3 => AD = 3R/2.

Отсюда OD = R/2;

AO ₁ = R и SO₁ = R; _

SD = √R² + R²/4 = R √5/2, _

OK₁ = 2* R *R/(2R√5) = R√5/5;

O₁K = R√5/5.

Из ∆O₁ FN => R² = (O₁K + x)² + NF²,

S_осн = 2NF². _

V_пр = S_осн*x = 2(R² – R ²/5 – 2 x√5 R/5 - x²)*x;

V_пр = 2(4R²x/5 – 2x²√5 R /5 - x³);

V’_пр(x) = 2 (4 R²/5 – 2x√5 R/5 - 3x ²) = 0; _

x _1,2 = (2 R√5/5 ⁺ √4R²/5 + 12R²/5)/(-3) = (2R√5/5 ⁺ 4R/√ 5)/(-3);

x = 2√5 R/15 _ _

V_{пр. ma x} = 2(4R²*2√5R/(5*1 5) – 2√5R*4R²/(45*5) - _ 40√5R³/(22 5 *15)) = 16R³√5(1 – 1/ 3 – 5/45)/75 = 16√5R³/135.

Ответ: 16√5R³/135 м³ при H = 2√5R/15.

Дано. ASO – конус;

SO = H;

AO = R;

CL/CM = BK/BN;

Найти. BN, чтобы V_пр = max

Решение. BN = x, CM = h, V_пр = S_осн CM = CL²h/2.

∆CSD подобен ∆ASO: CD/AO = SD/SO;

CD/R = (H – x - h)/H;

CD = R(H – x -h)/H.

∆BSE подобен ∆ASO: BE/AO = SE/SO;

BE/R = (H - h)/H;

BE = R(H - h)/H.

Находим отношение CD/BE = (H – x - h)/(H - x).

Исходя из условия (CL/CM = BK/BN) задачи делаем вывод,

что CD/BE = h/x, т. е. (H – x - h)/(H - x) = h/x => h = (Hx – x²)/H

Тогда CD = R(H – x – (Hx – x²)/H)/H = R(H² – Hx – Hx +x²)/H² = R(H - x)²/H²,

CL = 2CD = 2R(H - x)²/H².

V = 4R²(H - x)⁴(H - x)x/(2H*H⁴) = 2R²(H - x)⁵x/H⁵;

V’(x) = 2R²((H - x)⁵ – 5(H - x)⁴ x)/H⁵ = 0,

(H – x) – 5x = 0, x = H/6.

V = 2HR²(5H/6)⁵/(6H⁵) = 2R²H*5⁵/6⁶.

Ответ: при H/6, V_max = 2R²H*5⁵/6⁶.

В физике производная применяется в основном для вычисления наибольших или наименьших значений для каких-либо величин.

Задача 1. Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: U = a/r² – b/r, где a и b — положительные постоянные, r — расстояние между частицами.

Найти:

а) значение r₀ соответствующее равновесному положению частицы;

б) выяснить устойчиво ли это положение;

в) F_max значение силы притяжения;

г) изобразить примерные графики зависимости U(r) и F(r).

U = a/r² – b/r; Решение:

a и b — counts; Для определения r₀ соответствующего равновесному

r₀ —? положению частицы исследуем f = U(r) на экстремум.

F_max —? Используя связь между потенциальной энергией поля

U и F, тогда F = -dU/dr, получим F = -dU/dr = - (-2a/r³+b/r²) = 0;

при этом r = r₀; 2a/r³ = b/r² => r₀ = 2a/b;

Устойчивое или неустойчивое равновесие определим по знаку второй производной:

d²U/dr₀²= dF/dr₀=-6a/r₀⁴ + 2b/r₀³ = -6a/(2a/b)⁴+2b/(2a/b)³=(-b⁴/8a³)<0;

равновесие устойчивое.

Для определения F_max притяжения исследую на экстремумы функцию:

F = 2a/r³— b/r²;

dF/dr = -6a/r⁴ + 2b/ r³ = 0;

при r = r₁ = 3a/b;

подставляя, получу F_max = 2a/r³₁ — b/r³₁ = - b³/27a²;

U(r) = 0; при r = a/b; U(r)_min при r = 2, a/b = r₀;

F = 0; F(r)_max при r = r₁ = 3a/b;

Задача 2. Три резистора сопротивлениями R₁, R₂, R₃ соединены параллельно. Сопротивление R₁ в 9 раз больше сопротивления R₂. Если все три резистора соединить последовательно, то сопротивление цепи равно R.

Определить сопротивления резисторов при которых сопротивление исходной цепи будет наибольшим.

R₁ = 9 R₂ Решение:

При параллельном соединении резисторов эквивалентное

R₁, R₂, R₃ сопротивление по формуле:

1/R_экв = 1/R₁+1/R₂+1/R₃;

R_{экв max}—? выражу R₃ через R₂:

R₃ = R— R₁—R₂=R—10R₂;

тогда 1/R_экв = (10R—91R₂)/(9R₂(R—10R₂));

Задача сведена к определению наименьшего значения функции в интервале [0;R/10].

Возьмем производную от f(1/R_экв) по R₂ и преобразуем ее:

(1/R_экв)’ = -910(R₂—R/7)(R₂—R/13)/(9R₂² (R-10R₂)²);

В интересующем нас интервале только одна точка R₂ = R/13 в которой эта производная меняет знак с “—” слева на ”+”справа. Поэтому в точке R₂ = R/13 достигается минимум функции 1/R_экв и максимум функции R_экв, при этом

R₁ = 9R/13; R₂ = 1R/13; R₃ = 3R/13;

R_{экв max} = 9R/169;

Задача 4. В магнитном поле с большой высоты падает кольцо, имеющее диаметр d и сопротивление R. Плоскость кольца все время горизонтальна. Найти установившуюся скорость падения кольца, если вертикальная составляющая индукции магнитного поля изменяется с высотой H по закону B = B₀(1 + αH), где α = const (черт.).

Решение. Пусть n – нормаль к плоскости кольца, тогда магнитный поток, созданный вертикальной составляющей магнитного поля.,

Ф = BS = B₀(1 + αH)S, где S = πd²/4 – площадь контура.

ЭДС индукции, возникающая в кольце,

E = - Ф’(t) = - (B₀(1 + αH)S)’ = - B₀SαH’(t).

Производная H’(t) = ν_н – это проекция скорости кольца на ось H. Таким образом,

E_i = - B₀Sα(- ν_н).

Так как скорость кольца направлена против оси H, то ν_н = - ν, где ν – модуль скорости кольца и E_i = B₀Sαν.

По кольцу протекает индукционный ток

J = E_i /R = B₀Sαν/R.

В результате в кольце за промежуток времени Δt выделяется количество теплоты

Q = J²RΔt.

На высоте H₁ кольцо обладает механической энергией

W₁ = mgH₁ + mν²/2,

на высоте H₂

W₂ = mgH₂ = mgH₂ + mν²/2

(ν = const, т. е. скорость кольца не меняется). По закону сохранения энергии

W₁ = W₂ + Q => mgH₁ = mgH₂ + J²RΔt => mg(H₁ - H₂) = (B₀Sαν/R)²RΔt =>

mg(H₁ - H₂) = (B₀Sαν)²Δt/R (*)

Разность (H₁ - H₂) есть расстояние, пройденное кольцом при равномерном движении, поэтому H₁ - H₂ = νΔt, и уравнение (*) примет вид:

mgνΔt = (B₀Sαν)²Δt/R => mg = (B₀Sα)²ν/R =>

ν = mgR/(B₀Sα)² = 16mgR/(B₀πd²α)².

Ответ: ν = mgR/(B₀Sα)² = 16mgR/(B₀πd²α)².

Задача 6. Цепь с внешним сопротивлением R = 0,9 Ом питается от батареи из k=36 одинаковых источников, каждый из которых имеет ЭДС E=2 В и внутреннее сопротивление r₀ = 0,4 Ом. Батарея включает n групп, соединенных параллельно, а в каждой из них содержится m последовательно соединенных аккумуляторов. При каких значениях m, n будет получена максимальная J во внешнем R (см. рис.).

Решение:

При последовательном соединении аккумуляторов E _гр = m* E; r_гр = r₀*m;

а при параллельном соединении одинаковых r_бат = r₀m/n; E _бат = m* E,

По закону Ома J = m E /(R+ r₀m/n) = m E n/(nR + r₀m)

Т.к. k – общее число аккумуляторов, то k = mn;

J = kE/(nR + r₀m) = kE/(nR + kr₀/n);

Для нахождения условия при котором J тока в цепи максимальная исследую функцию J = J(n) на экстремум взяв производную по n и приравняв ее к нулю.

J’_n-(kE(R—kr₀/n²))/ (nR + kr₀/n)² = 0;

n² = kr/R ;.

n = √kr/R = √3,6*0,4/0,9 = 4;

m = k/n = 36/4 = 9;

при этом J_max = k E /(nR + mr₀) = 36*2/(4*0,9 + 9*0,4) = 10 А;

Ответ: n = 4, m = 9.

Задача 7. Платформа массой М начинает двигаться вправо под действием постоянной силы F. Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна m кг/с. Пренебрегая трением, найти зависимость от времени ускорения а платформы в процессе погрузки. Определить ускорение а₁ платформы в случае, если песок не насыпается на платформу, а из наполненной высыпается через отверстие в ее дне с постоянной скоростью m кг/с.

Решение.

Рассмотрим сначала случай, когда песок насыпается на платформу

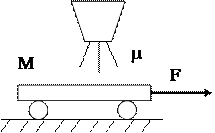Движение системы платформа-песок можно описать с помощью второго закона Ньютона:

dP/dt = F_S

P – импульс системы платформа-песок, F_S – сила, действующая на систему платформа-песок.

Если через p обозначить импульс платформы, то можно написать:

dp/dt = F

Найдем изменение импульса платформы за бесконечно малый промежуток времени Dt:

Dp = (M+m(t+Dt))(u+Du) – (M+mt)u =FDt

где u – скорость платформы

Раскрыв скобки и, проведя сокращения получаем:

Dp = muDt + MDu+mDut+ mDuDt =FDt

Разделим на Dt и перейдем к пределу Dt ®0

Mdu/dt+mtdu/dt+mu=F

или

d[(M+mt)u]/dt = F

Это уравнение можно проинтегрировать, считая начальную скорость платформы равной нулю:

(M+mt)u = Ft

Следовательно:

u = Ft/(M+mt)

Тогда, ускорение платформы:

a = du/dt = (F(M+mt)-Ftm)/(M+mt)² = FM / (M+mt)²

Рассмотрим случай, когда песок высыпается из наполненной платформы.

Изменение импульса за малый промежуток времени:

Dp = (M-m(t+Dt))(u+Du) +mDtu – (M-mt)u = FDt

Слагаемое mDtu есть импульс количества песка, которое высыпалось из платформы за время Dt

Тогда:

Dp = MDu - mtDu - mDtDu = FDt

Разделим на Dt и перейдем к пределу Dt ®0

(M-mt)du/dt = F

или

a₁=du/dt= F/(M-mt)

Ответ: a = FM / (M+mt)², a₁= F/(M-mt)

Поиск по сайту: