АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формула Тейлора

Читайте также:
  1. Барометрическая формула
  2. Барометрическая формула. Распределение Больцмана.
  3. Биография Ф.Тейлора
  4. Визначити енергію вибуху балону. Формула (3)
  5. Внешний фотоэффект и его законы. Формула Эйнштейна для фотоэффекта.
  6. Вопрос 2 Формула апостериорной вероятности Байеса
  7. Вопрос 2 Формула апостериорной вероятности Байеса.
  8. Вопрос 2 Формула апостериорной вероятности Байеса.
  9. Дифракция на трехмерных структурах. Формула Вульфа-Брэггов. Рентгеноструктурный анализ. Понятие о голографии.
  10. Из формулы (8.4) следует формула Байеса
  11. Интерполяционная формула Ньютона.
  12. Какая формула соответствует общему индексу цен Ласпейреса

В просторі 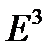візьмемо ортонормований базис , і розкладемо за ним вектор-функцію : .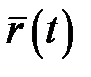

Нехай функції в околі точки t0 , мають скінченні похідні до -го порядку включно.

Для кожної скалярної функції , , запишемо формулу Тейлора в околі точки t0 зі своїм залишковим членом та своєю проміжною точкою 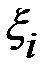(i = 1,2,3):

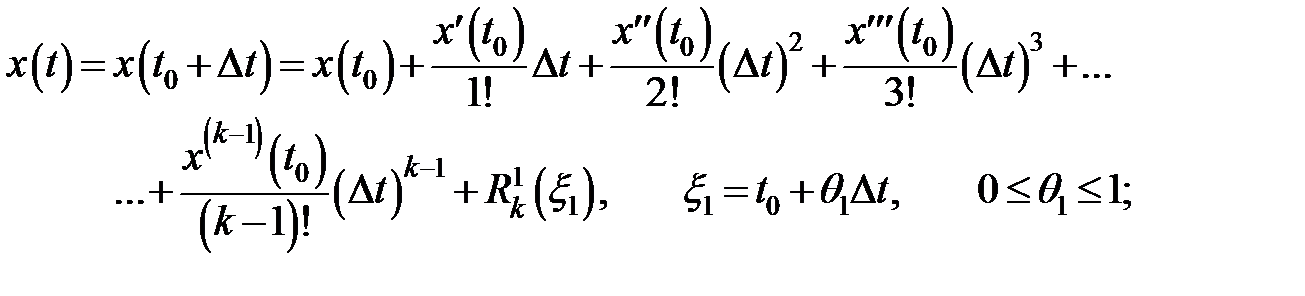
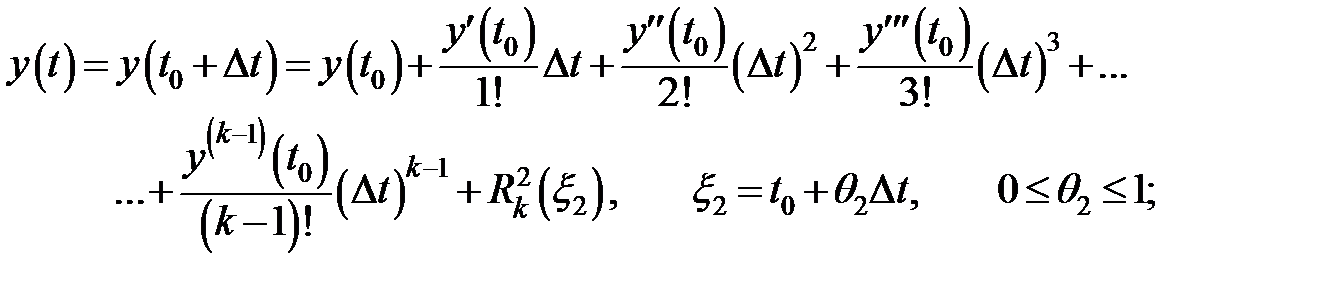
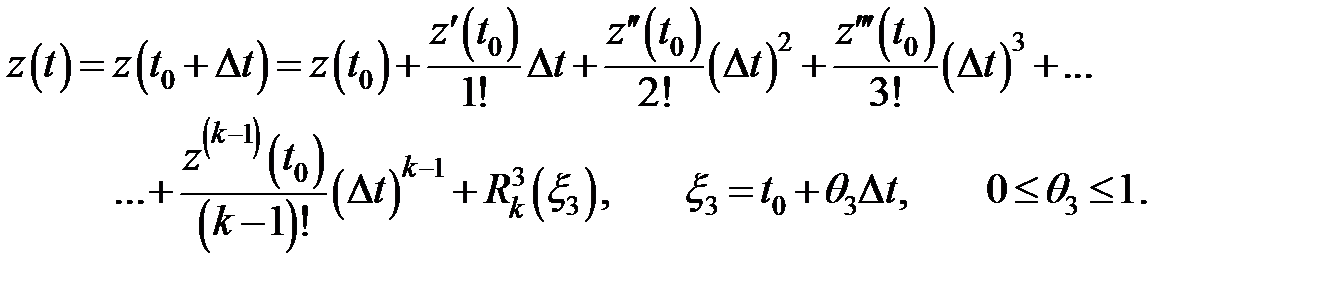
Помножимо рівності для , , відповідно на та додамо:

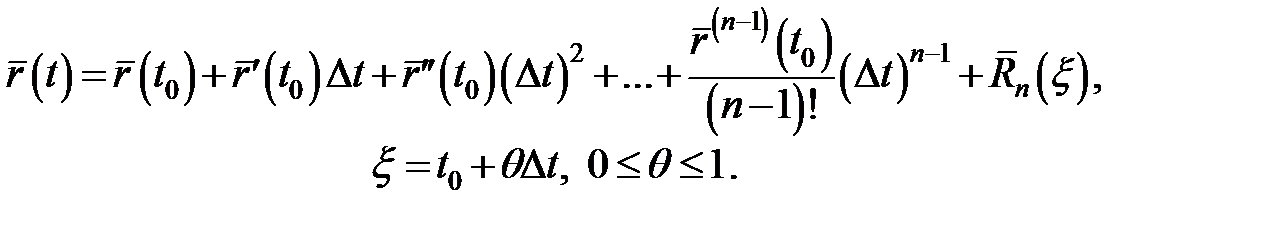
Якщо 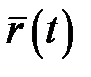має похідні довільного порядку, для неї можна скласти формальний ряд Тейлора в околі точки t0:

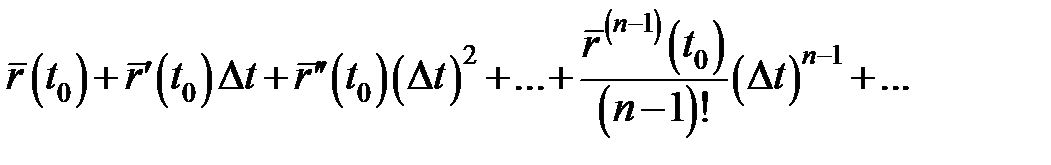
Не кожний формальний ряд Тейлора збігається.

Аналітичною вектор-функцією у точці називається функція, яка має в цій точці похідні будь-якого порядку та існує окіл точки t0, в якому ряд Тейлора збігається до функції .

Позначення: 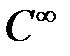– клас аналітичних функцій.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)