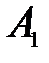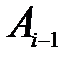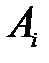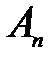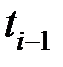|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Довжина дуги кривої. Натуральна параметризація
Нехай просторову криву γ дано параметричним рівнянням 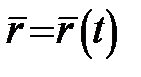 і
і 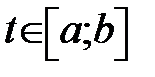 . Впишемо в криву
. Впишемо в криву  ламану.
ламану.

 , якщо її вершини на кривій слідують в тому ж порядку (тобто без зворотів), що і їх прообрази на відрізку , якщо її вершини на кривій слідують в тому ж порядку (тобто без зворотів), що і їх прообрази на відрізку  . .
|
На відрізку 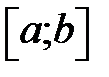 візьмемо точки
візьмемо точки 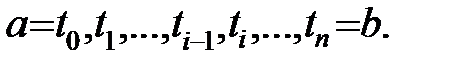 На кривій γ їм відповідають точки
На кривій γ їм відповідають точки 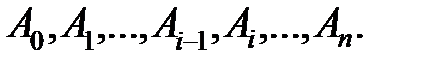 Сполучаючи послідовно ці точки, одержимо ламану
Сполучаючи послідовно ці точки, одержимо ламану 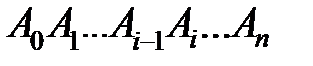 , вписану в криву
, вписану в криву  .
.
Розглянемо довжину цієї ламаної. Якщо кількість вершин ламаної збільшується, то її довжина збільшується. Справді, якщо на дузі кривої  з кінцями
з кінцями  і
і 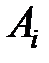 взято нову вершину C, то сума прямолінійних відрізків
взято нову вершину C, то сума прямолінійних відрізків  і
і 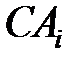 більша довжини прямолінійного відрізка
більша довжини прямолінійного відрізка 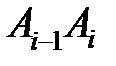 . Тому довжина нової вписаної ламаної
. Тому довжина нової вписаної ламаної 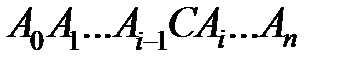 більша довжини ламаної
більша довжини ламаної 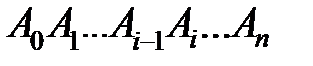 .
.
Крива γ називається спрямною, якщо довжини всіх правильно вписаних в неї ламаних обмежені зверху.
Верхня границя довжин усіх таких ламаних називається довжиною кривої  і позначається і позначається 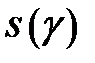 . .
|
Вона існує за теоремою Вейєрштраса.
Теорема 7. Гладка крива є спрямною. Довжина 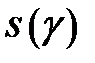 гладкої кривої гладкої кривої 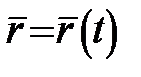 ( ( ) дорівнює визначеному інтегралу від модуля похідної ) дорівнює визначеному інтегралу від модуля похідної  : :
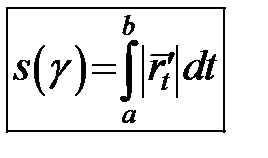 . (11) . (11)
|
В скалярній формі формула (11) має вид:
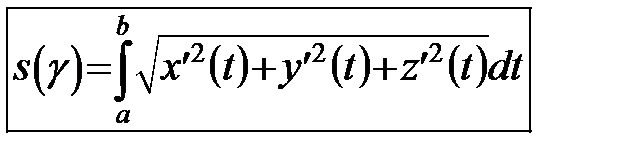 . (12)
. (12)
Якщо криву задано рівняннями 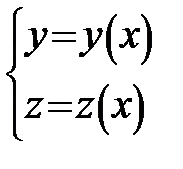 , то
, то 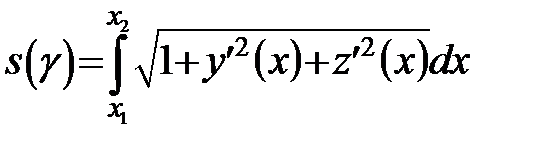 .
.
Для плоских кривих, розміщених у координатній площині 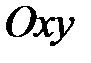 , в цих формулах слід покласти
, в цих формулах слід покласти  .
.
Поняття довжини кривої дозволяє визначити на кривій параметр, який найбільш природнім способом пов’язаний з кривою. Таким параметром є довжина дуги. Дійсно, виберемо на кривій точку 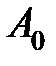 і який-небудь напрямок на ній. Положення точки B на кривій визначається її відстанню від точки
і який-небудь напрямок на ній. Положення точки B на кривій визначається її відстанню від точки 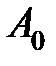 . Приймемо за параметр на кривій довжину s дуги
. Приймемо за параметр на кривій довжину s дуги 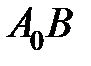 , взяту зі знаком +, якщо дуга
, взяту зі знаком +, якщо дуга 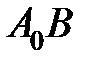 має додатній напрямок, і зі знаком –, якщо дуга
має додатній напрямок, і зі знаком –, якщо дуга 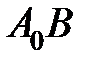 має від’ємний напрямок.
має від’ємний напрямок.
Якщо до цього на прямій була інша параметризація 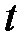 і точці
і точці 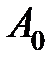 відповідало значення
відповідало значення 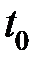 , а точці B – значення
, а точці B – значення 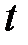 , то довжина
, то довжина 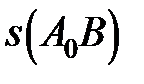 обчислюється за формулою:
обчислюється за формулою:
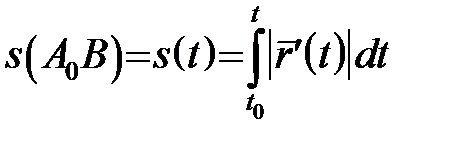 , а отже
, а отже 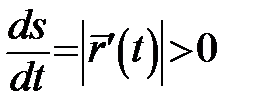 , тобто
, тобто 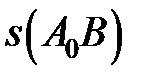 є монотонною функцією від параметра
є монотонною функцією від параметра  і може бути прийнята за параметр. Цей параметр особливо зручний для вивчення кривої за її рівнянням і називається натуральним параметром кривої. Така параметризація називається натуральною і позначається
і може бути прийнята за параметр. Цей параметр особливо зручний для вивчення кривої за її рівнянням і називається натуральним параметром кривої. Така параметризація називається натуральною і позначається 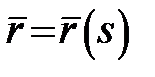 .
.
Для натуральної параметризації дотичний вектор кривої  є одиничним вектором, тобто
є одиничним вектором, тобто 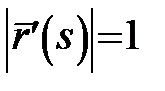 . Дійсно:
. Дійсно:  .
.
Визначна властивість натуральної параметризації:
Якщо 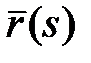 – натуральна параметризація, то – натуральна параметризація, то 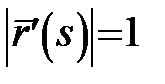 .
Навпаки, якщо для деякого параметра .
Навпаки, якщо для деякого параметра 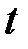 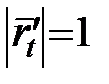 , то , то 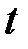 – довжина дуги. – довжина дуги.
|
4.2. Кривина кривої, заданої в натуральній параметризації

|
|
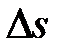
|
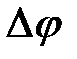
|
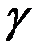
|
| Рис.15 |
 будь-яку точку P і точку Q, близьку до P. Проведемо дотичні в точках P і Q, знайдемо кут між ними і поділимо цей кут на довжину дуги PQ.
будь-яку точку P і точку Q, близьку до P. Проведемо дотичні в точках P і Q, знайдемо кут між ними і поділимо цей кут на довжину дуги PQ.
Позначимо:
 – кут між дотичними до γ в точках P і Q,
– кут між дотичними до γ в точках P і Q, 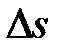 – довжина дуги PQ кривої γ.
– довжина дуги PQ кривої γ.
Кривиною 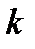 кривої γ в точці P називається границя відношення кута повороту дотичної на дузі, що стягується до даної точки, до довжини цієї дуги, тобто кривої γ в точці P називається границя відношення кута повороту дотичної на дузі, що стягується до даної точки, до довжини цієї дуги, тобто
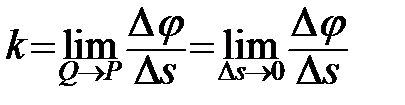 . .
|
| Q |
| P |
| O |
| Рис. 16 |
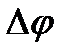
|
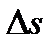
|
Для кола радіуса R: 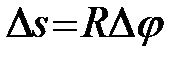 . Тому
. Тому 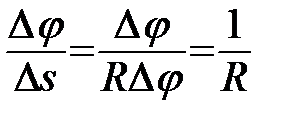 незалежно від Q. Отже, кривина кола є сталою і дорівнює
незалежно від Q. Отже, кривина кола є сталою і дорівнює  , де R – радіус кола.
, де R – радіус кола.
Вектор 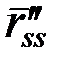 називається вектором кривини кривої. Його довжина дорівнює кривині називається вектором кривини кривої. Його довжина дорівнює кривині 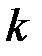 кривої, заданої в натуральній параметризації. кривої, заданої в натуральній параметризації.
|
Теорема 8. Регулярна кривакласу 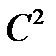 (двічі неперервнодиференційовна) має в кожній точці єдину кривину. Якщо (двічі неперервнодиференційовна) має в кожній точці єдину кривину. Якщо 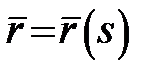 – натуральна параметризація кривої, то кривина дорівнює модулю другої похідної функції – натуральна параметризація кривої, то кривина дорівнює модулю другої похідної функції 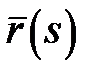 : :  . .
|
|

|
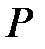
|
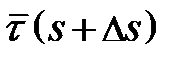
|
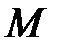
|
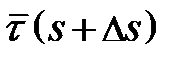
|
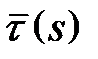
|

|
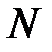
|
| Рис.17 |
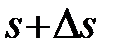 відповідно. Нехай
відповідно. Нехай 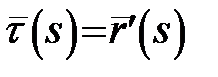 і
і 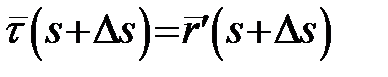 – одиничні дотичні вектори кривої в цих точках. Вектор
– одиничні дотичні вектори кривої в цих точках. Вектор 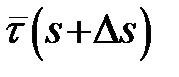 перенесемо паралельно так, щоб його початок співпадав з точкою P. Кінці векторів
перенесемо паралельно так, щоб його початок співпадав з точкою P. Кінці векторів 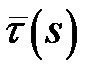 і
і 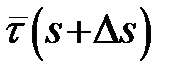 позначимо M і N. ∆ PMN – рівнобедрений, бо вектори
позначимо M і N. ∆ PMN – рівнобедрений, бо вектори 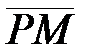 і
і  – одиничні.
– одиничні.
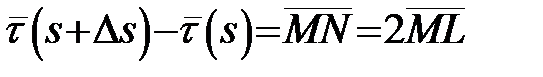 , де L – середина відрізка MN.
, де L – середина відрізка MN.
З прямокутного трикутника PML, де 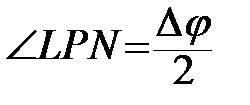 :
: 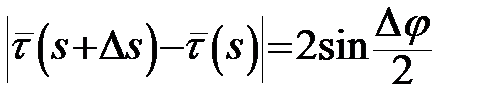 .
.
Поділимо обидві частини цієї рівності на 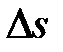 і перейдемо до границі при
і перейдемо до границі при 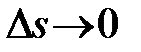 .
.
Оскільки  – двічі неперервно диференційовна крива і
– двічі неперервно диференційовна крива і  , то існує
, то існує
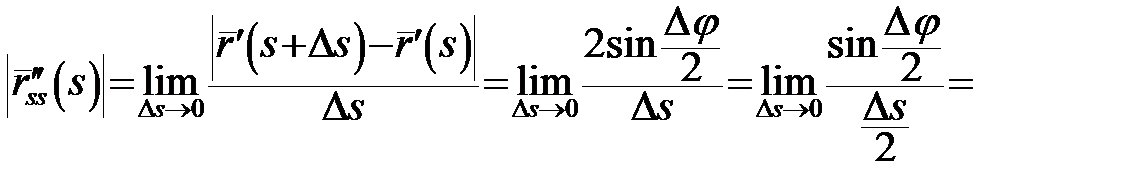
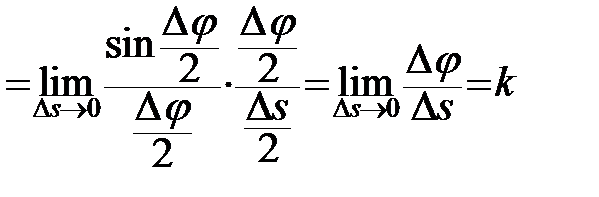 ,
,
бо 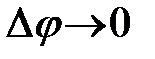 при
при 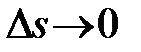 і границя першого множника дорівнює 1 (перша чудова границя). ■
і границя першого множника дорівнює 1 (перша чудова границя). ■
Нехай в даній точці кривина 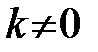 . Розглянемо властивості вектора
. Розглянемо властивості вектора 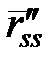
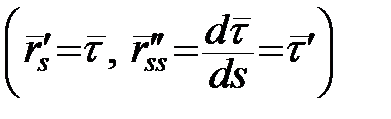 :
:
1)  (оскільки
(оскільки  – одиничний вектор і
– одиничний вектор і 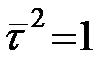 , отже
, отже 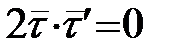 );
);
2) 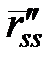 належить стичній площині;
належить стичній площині;
3) 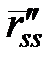 напрямлений за головною нормаллю і
напрямлений за головною нормаллю і 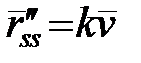 де
де 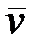 – одиничний вектор головної нормалі. Останню рівність можна подати у виді:
– одиничний вектор головної нормалі. Останню рівність можна подати у виді:
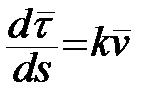 (перша формула Френе). (13)
(перша формула Френе). (13)
4.3. Кривина кривої в довільній параметризації
Нехай криву задано векторним рівнянням 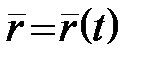 . Довжина дуги s є функцією параметра
. Довжина дуги s є функцією параметра 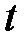 :
: 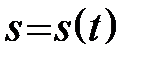 , отже
, отже 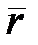 є складеною функцією
є складеною функцією 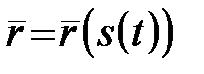 . Знайдемо другу похідну від
. Знайдемо другу похідну від 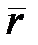 по s через похідні по t.
по s через похідні по t.
Для зручності домовимося похідні вектор-функції по натуральному параметру s позначати з крапкою (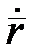 ,
, 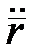 і т.д.), а похідні по довільному параметру t – зі штрихом (
і т.д.), а похідні по довільному параметру t – зі штрихом ( ,
,  і т.д.).
і т.д.).
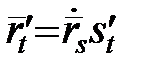 ; (14)
; (14)
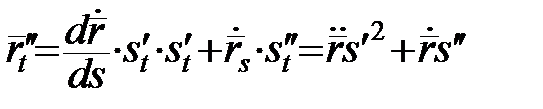 , звідки
, звідки  . (15)
. (15)
З (14) маємо:  , причому
, причому 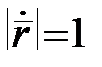 .
.
Враховуючи, що 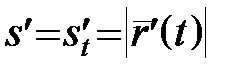 , одержимо
, одержимо  .
.
Підставимо одержані вирази для 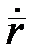 ,
, 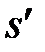 ,
, 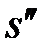 в (15):
в (15):
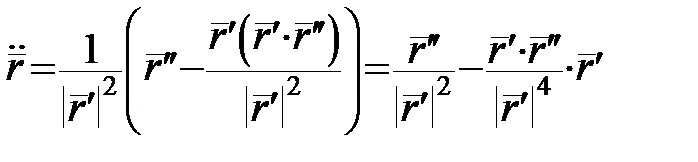 .
.
Для обчислення кривини 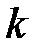 знайдемо
знайдемо 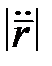 .
.
Оскільки  – одиничний вектор і його похідна
– одиничний вектор і його похідна 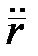 ортогональна
ортогональна  , то
, то 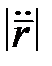 можна знайти як модуль векторного добутку
можна знайти як модуль векторного добутку 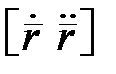 :
: 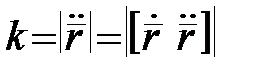 .
.
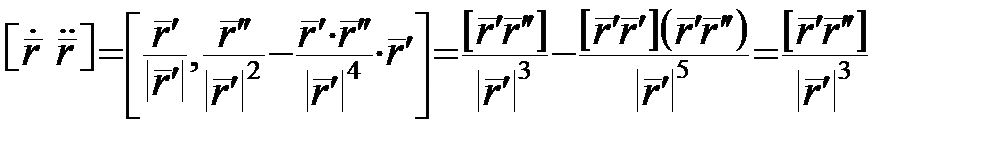 .
.
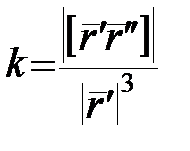 (16)
(16)
В скалярній формі маємо:
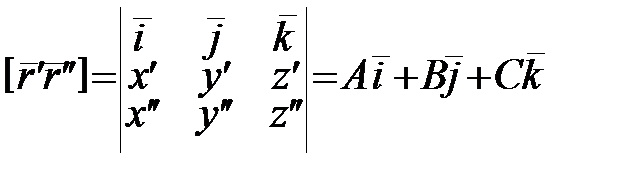 , де A, B, C – координати вектора
, де A, B, C – координати вектора  , тобто
, тобто
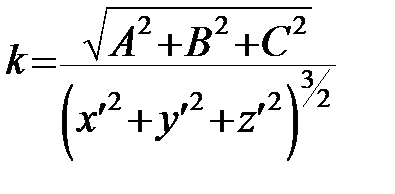 (16')
(16')
Задача. Знайти кривину гвинтової лінії 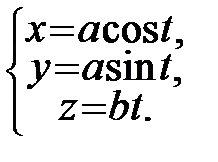
Розв’язання.
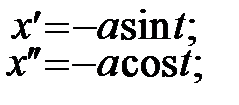
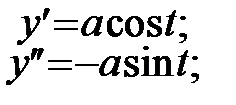
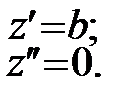
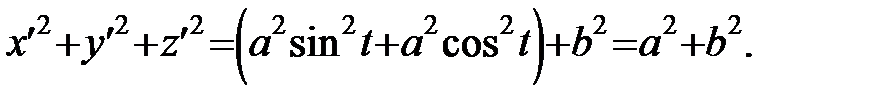
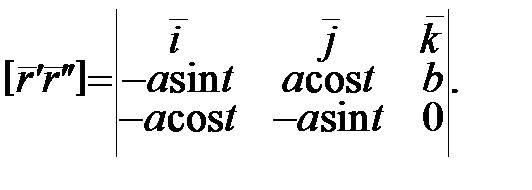
Отже  ;
;  ;
; 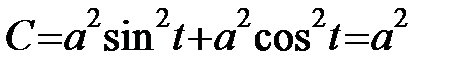 ;
;
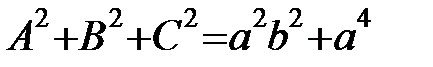 .
.
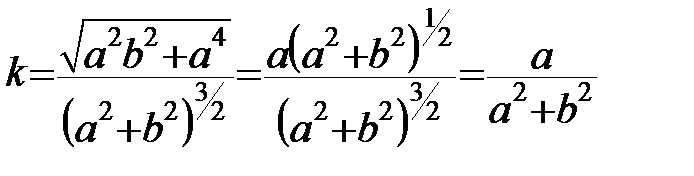
Таким чином, кривина гвинтової лінії є сталою величиною.
Відповідь: 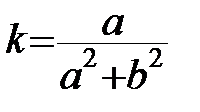 .
.
4.4. Кривина плоскої кривої
З формул (16) і (16') легко одержати формули для обчислення кривини плоскої кривої:
1) 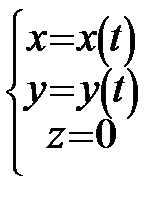 :
: 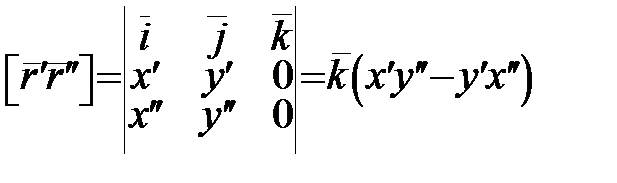 ;
; 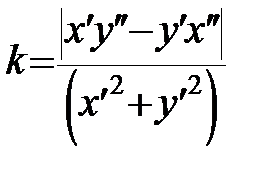 . (17)
. (17)
2) 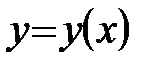 :
: 
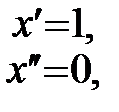


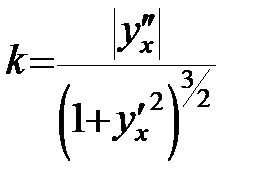 . (17')
. (17') 
3) 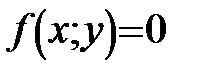 : вважаємо що y є функцією від x, диференціюємо дане рівняння по x, звідки
: вважаємо що y є функцією від x, диференціюємо дане рівняння по x, звідки 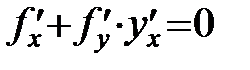 і
і 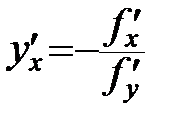 ; далі знаходимо
; далі знаходимо 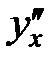 і підставляємо у формулу (17').
і підставляємо у формулу (17').
Поиск по сайту: