 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Границя вектор-функції
|
Читайте также: |
Нехай вектор-функція 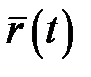 визначена в деякому околі точки визначена в деякому околі точки  , крім, можливо, самої точки , крім, можливо, самої точки  .Сталий вектор .Сталий вектор  називається границею вектор-функції називається границею вектор-функції 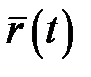 при при 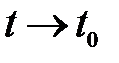 , якщо різниця між ними є нескінченно малим вектором: , якщо різниця між ними є нескінченно малим вектором:  , тобто , тобто
 . .
|
Позначення: 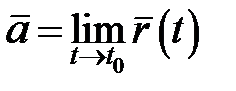 .
.
Отже, кожну вектор-функцію можна подати як суму границі і нескінченно малого вектора:  .
.
Теореми про границі
Теорема 1.Якщо границі вектор-функцій  і скалярної функції і скалярної функції  існують, то
1. існують, то
1.  ;
2. ;
2. 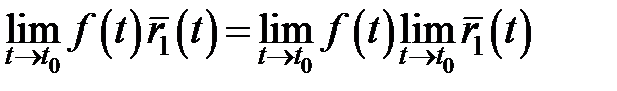 ;
3. ;
3.  ;
4. ;
4.  ;
5. ;
5. 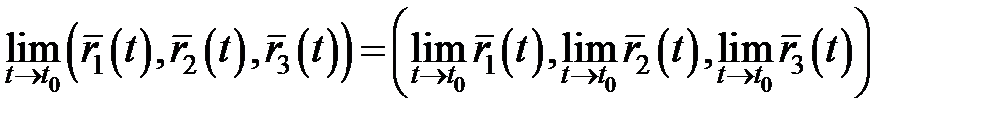 ;
6. ;
6.  ;
7. ;
7.  . .
|
Доведемо, наприклад, властивість 4.
□ Згідно з умовою теореми й означенням границі вектор-функції маємо:
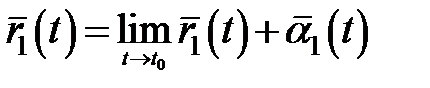 ,
, 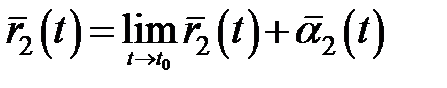 .
.
Тоді

 . ■
. ■
Поиск по сайту: