Границя функції декількох змінних

Введемо спочатку важливе поняття околу точки.

Означення 1.3. Околом ( - околом) точки називатимемо множину всіх точок M, таких що .

З цього означення випливає, що на площині - околом точки буде множина всіх тих точок , для яких , тобто відкритий круг з радіусом і центром в точці (рис. 1.4), а в просторі - околом точки буде множина всіх точок , для яких , тобто відкрита куля з радіусом і центром в точці .

Надалі - окіл точки позначатимемо .

Зауваження 1.4. Якщо з - околу точки викинуто саму точку , то такий окіл називатимемо проколотим околом ( - околом) і позначатимемо .

Означення 1.4. Точка називається внутрішньою точкою множини D, якщо вона належить цій множині разом зі своїм деяким околом.

Означення 1.5. Точка називається межовою точкою множини D, якщо в будь-якому її проколотому околі є точки, які належать цій множині і є точки, які їй не належать.

Тепер можемо дати означення границі функції в точці.

Означення 1.6. Нехай функція двох змінних визначена в деякій області D, для якої точка є внутрішньою або межовою. Число A називається границею функції в точці при , якщо для довільного знайдеться таке , що для всіх точок має місце нерівність

. (1.4)

Це записують таким чином:

. (1.5)

Умова означає або , що в свою чергу рівносильне такому: 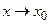та . Тоді рівність (1.5) можна записати ще й так:

. (1.6)

Зауваження 1.5. З наведеного вище означення випливає, що в випадку існування границі функції декількох змінних в точці ми отримуватимемо те саме значення границі, рухаючись до точки вздовж довільної лінії в межах області визначення функції. Відповідно, якщо нам вдасться вказати хоча б дві лінії, рухаючись вздовж яких до точки , ми отримаємо різні значення границь, то звідси випливатиме, що в точці границя функції не існує.

Зауваження 1.6. Всі відомі теореми про границі для функцій однієї змінної узагальнюються на випадок функцій декількох змінних. Доведення цих теорем ми опускаємо, оскільки вони майже не відрізняються від доведення відповідних теорем для функцій однієї змінної.

Розглянемо приклади.

Приклад 1.6. Знайти границю .

Використовуючи властивість границі для добутку функцій, а також першу важливу границю, матимемо:

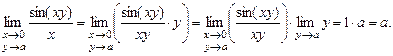
Приклад 1.7. Знайти границю .

З очевидної нерівності отримуємо . Звідси, при , отримаємо

.

Оскільки та , то за теоремою про границю проміжної функції .

Приклад 1.8. Розглянемо функцію

Вона визначена в усіх точках площини. Покажемо, що ця функція в точці О(0;0) границі не має. Як уже відзначалось, для цього достатньо вказати два напрямки, рухаючись вздовж яких до точки О (0;0), отримуємо різні значення границь. Дійсно, вздовж прямої маємо , тому й ; а вздовж прямої маємо , тому й .

Поиск по сайту: