Змінних. Необхідні умови екстремуму

Як і для функції однієї змінної, для функції декількох змінних вводять поняття екстремальної точки.

Нехай функція декількох змінних визначена в деякій області D, для якої точка 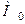внутрішня.

Означення 5.1. Якщо існує проколотий окіл точки 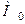, який повністю міститься в області D, і для всіх точок М з цього проколотого околу значення функції в точці М менше (більше) за значення функції в точці 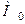, то точка 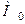називається точкою локального максимуму (мінімуму) заданої функції, а значення самої функції в точці 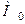називається локальним максимумом (мінімумом) функції.

Точки локального максимуму чи мінімуму називають точками локального екстремуму, а максимум чи мінімум - локальним екстремумом даної функції.

Надалі, з метою більшої зручності викладок, слово локальний опускатимемо.

Як і раніше, для простоти розглядатимемо функцію двох змінних.

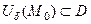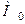Отже, відповідно до означення 5.1, точка , яка є внутрішньою для області визначення функції , буде точкою максимуму (мінімуму) цієї функції, якщо знайдеться такий окіл , що для всіх точок , відмінних від точки , виконується нерівність

(5.1)

Приклад 5.1. Розглянемо деякі функції.

1. Для функції

, (5.2)

визначеної в усіх точках площини, для довільної точки , як легко бачити, виконується нерівність

,

отже, 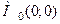- точка мінімуму для заданої функції.

2. Оскільки для функції

, (5.3)

також визначеної в усій площині, для довільної точки має місце нерівність

,

то - точка максимуму для функції (5.3).

3. Для функції

, (5.4)

визначеної в усіх точках площини, в будь-якому околі точки 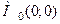є точки

виду і . Так як

,

то точка 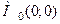не може бути ні точкою максимуму, ні точкою мінімуму для заданої функції (5.4).

Виникає запитання, як знаходити екстремальні точки функції , якщо вони існують. Зрозуміло, що ці точки будуть серед точок, підозрілих на екстремум. Для знаходження таких точок використовують необхідні умови існування екстремуму функції.

Теорема 5.1. Якщо точка є точкою екстремуму для функції і в цій точці існують частинні похідні 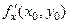, , 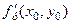то вони дорівнюють нулю:

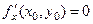, . (5.5)

Д о в е д е н н я. Зафіксуємо в функції змінну у, поклавши . Тоді наша функція перетвориться в функцію однієї змінної х:

Очевидно, для функції точка 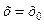є точкою екстремуму. Також, відповідно до умов теореми, ця функція в точці 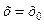має похідну

.

Тоді, згідно необхідної умови екстремуму для функції однієї змінної, 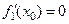, звідки робимо висновок, що .

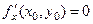Аналогічно доводимо, що . Тим самим теорему доведено.

Означення 5.2. Точка, в якій усі частинні похідні функції декількох змінних дорівнюють нулю, називається стаціонарною точкою даної функції.

Отже, стаціонарна точка може бути точкою екстремуму. Щоб знайти стаціонарні точки функції , потрібно розв¢язати систему рівнянь

(5.6)

Приклад 5.2. Знайти стаціонарні точки функції .

Р о з в′ я з а н н я

Частинні похідні заданої функції дорівнюють:

, .

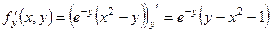Тоді система рівнянь (5.6) матиме вигляд:

З першого рівняння легко отримуємо . Тоді з другого рівняння маємо .

Отже, для заданої функції точка 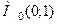є стаціонарною. Інших стаціонарних точок немає.

Зауваження 5.1. Не кожна стаціонарна точка для зада-ної функції є точкою екстремуму цієї функції, тобто необхідні умови екстремуму не є достатніми. Дійсно, як ми побачили в прикладі 5.1, точка 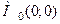не є точкою екстремуму для функції (5.4), хоча , звідки , , тому точка 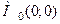є стаціонарною.

Поиск по сайту: