Достатні умови екстремуму

Розглянемо умови, які гарантують екстремум функції декількох змінних в заданій точці.

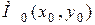Теорема 5.2. Нехай для функції точка є стаціонарною і в деякому околі цієї точки дана функція має неперервні частинні похідні до другого порядку включно.

Тоді якщо

,

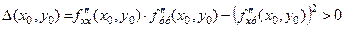то функція в точці 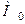має екстремум, причому максимум при 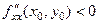і мінімум при .

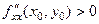Якщо , то функція в стаціонарній точці 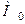екстремуму не має.

Д о в е д е н н я. Оскільки функція в околі стаціонарної точки 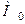має неперервні частинні похідні до другого порядку включно, то її можна розвинути за формулою Тейлора першого порядку з залишковим членом в формі Лагранжа:

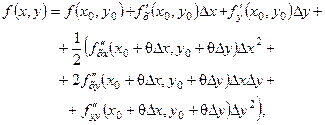(5.7)

де , .

Так як частинні похідні другого порядку є неперервними функціями в околі точки , то

(5.8)

де 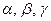- функції від 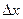та 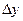, такі що

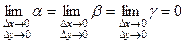. (5.9)

Позначимо для зручності

.

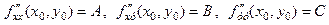Точка є стаціонарною, тобто 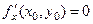, , тому, враховуючи (5.8), рівність (5.7) можна записати так:

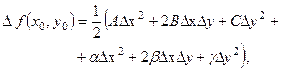(5.10)

де

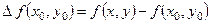(5.11)

- повний приріст функції в точці .

Нехай - кут, який утворює вектор з додатнім напрямком осі Ох, 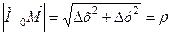. Тоді і рівність (5.10) набуде такого вигляду:

(5.12)

Розглянемо тепер два випадки.

1) .

Тоді обов¢язково і суму перших трьох доданків у співвідношенні (5.12) можемо записати так:

(5.13)

Очевидно, що вираз у зовнішніх дужках є строго додатним при усіх значеннях . Тому функція, що являє собою ліву частину рівності (5.13), набуває ненульових значень, які за знаком збігаються зі знаком числа А, для всіх . Оскільки 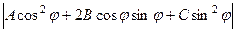є функцією, неперервною на відрізку , то вона на цьому відрізку набуває найменшого значення m, яке є, зрозуміло, додатним, тобто

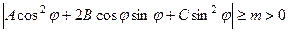. (5.14)

Так як 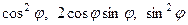- обмежені, то, враховуючи (5.9), маємо

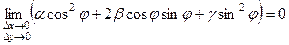, (5.15)

тобто існує такий окіл 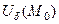, що для всіх точок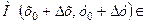 виконується нерівність

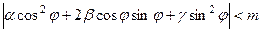. (5.16)

Тоді з рівності (5.12), а також з нерівностей (5.14) та (5.16) видно, що для всіх точок 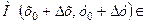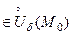значення збігається за знаком зі знаком числа .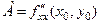

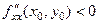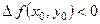Отже, якщо , то або

,

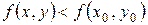тобто в стаціонарній точці функція має максимум.

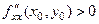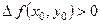Якщо ж , то або

,

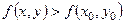тобто в стаціонарній точці функція має мінімум.

2) .

Якщо число то виконується рівність (5.13). Очевидно, при 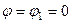вираз у дужках співвідношення (5.13) дорівнює , тобто додатний.

Нехай 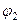- один з коренів рівняння

.

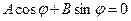Тоді обов'язково , тому при 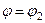вираз у дужках співвідношення (5.13) від¢ємний, бо дорівнює .

На основі рівності (5.15) при досить малих значеннях 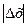та 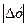знак виразу в дужках правої частини рівності (5.12) співпадатиме зі знаком виразу (5.13). Отже, приріст на променях 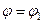та 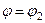матиме значення протилежних знаків. Тому точка не може бути точкою екстремуму.

Якщо число то

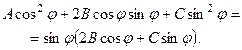(5.17)

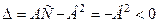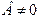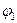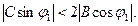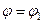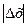Так як , то , тому можемо вибрати такий кут , що Тоді на променях та вираз (5.17), знаком якого при досить малих значеннях та 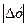визначається знак , матиме значення, протилежні за знаком. Значить, приріст на променях 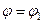та матиме значення протилежних знаків, тому точка не буде екстремальною.

Теорему доведено.

Зауваження 5.2. У випадку, коли 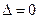, теорема 5.2 не дає відповіді на питання, чи є стаціонарна точка точкою екстремуму. Ми цей випадок не досліджуватимемо. Відзначимо тільки, що в точці 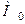може бути екстремум, а може і не бути.

З теорем 5.1 та 5.2 випливає таке правило дослідження функції двох змінних на екстремум:

1) знаходимо стаціонарні точки даної функції, розв¢язуючи систему рівнянь (5.6);

2) для кожної стаціонарної точки обчислюємо число .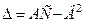

Якщо в стаціонарній точці 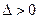, то ця точка є точкою екстремуму, причому точкою максимуму при 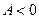або точкою мінімуму при .

Якщо в стаціонарній точці , то ця точка не є точкою екстремуму.

Розглянемо приклади.

Приклад 5.3. Для функції , розглянутої в прикладі 5.1, як ми бачили, точка 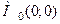не є точкою екстремуму, хоча вона є стаціонарною (зауваження 5.1).

Частинні похідні другого порядку дорівнюють:

.

.

Значить, в усіх точках площини, зокрема і в стаціонарній точці 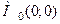. Отже, теорема 5.2 підтверджує, що ця стаціонарна точка не є екстремальною для заданої функції.

Приклад 5.4. Дослідити на екстремум функцію .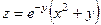

Р о з в′ я з а н н я

В прикладі 5.2 ми встановили, що задана функція має одну стаціонарну точку 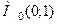. Знайдемо частинні похідні другого порядку в цій точці.

, ;

, ;

.

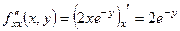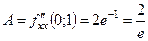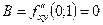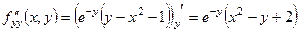
Тоді 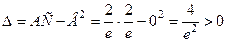. Значить, точка 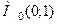є екстремальною для заданої функції, а саме точкою мінімуму, бо .

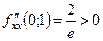Цей мінімум дорівнює .

Поиск по сайту: