АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Лінії та поверхні рівня

Читайте также:
  1. Більшовизм та марксизм: порівняльний аналіз
  2. Бюджетні обмеження споживача, бюджетне рівняння та фактори впливу на бюджетну лінію.
  3. Валютний ринок і валютні курси. Системи гнучких і фіксованих валютних курсів: порівняльна ефективність
  4. Вивченням власних імен людей займається порівняно молода ще наука – антропоніміка.
  5. Визначення гранично-допустимого рівня небезпечного фактору.
  6. Визначення критичної суми постійних витрат, змінних витрат на одиницю продукції і критичного рівня ціни реалізації
  7. Визначення порівняльної економічної ефективності капіталовкладень
  8. Вирішення алгебричних рівнянь графічним методом за допомогою Simulink
  9. Вирішення диференційних рівнянь символічній формі
  10. Вирішення систем алгебричних рівнянь у символічній формі
  11. Вирішення систем диференційних рівнянь у символічній формі
  12. Вкажіть номер неправильної відповіді. Аварійні події на АЕС за збільшенням тяжкість класифікується по рівнях шкалою МАГАТЕ 1990г.

Більш наочним способом геометричного функції двох змінних порівняно з побудовою її графіка є спосіб за допомогою ліній однакового рівня.

Нехай функцію зображено деякою поверхнею. Перетнувши цю поверхню площиною , отримаємо деяку поверхню. Ортогональна проекція її на площину називається лінією рівня функції . Зрозуміло, що рівняння лінії рівня в площині матиме вигляд .

Надаючи с різних дійсних значень, щоразу діставатимемо на площині різні лінії рівня.

Чим більше побудовано ліній рівня, тим яскравіше можна уявити характер зміни функції, а саме, в тій частині області визначення функції, де густіше розміщені лінії рівня, функція швидше змінюється (частина поверхні крутіша), а там, де лінії рівня розміщені рідше, функція змінюється повільніше (частина поверхні пологіша).

Приклад 1.4. Для функції 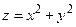рівняння ліній рівня

матимуть вигляд

.

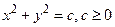Очевидно, що це є рівняння кіл з центрами в початку координат і радіусами

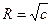. Отже, лініями рівня функції є концентричні кола (рис. 1.3).

Як уже відзначалось, функцію трьох змінних графічно зобразити не можна. Разом з тим, множина точок простору, в яких функція трьох змінних приймає одне і те саме значення, утворить деяку поверхню, яка називається поверхнею рівня. Таким чином, рівняння поверхні рівня для функції (1.2) матиме вигляд

.

Приклад 1.5. Для функції рівняння поверхонь рівня матимуть вигляд

. (1.3)

При рівняння (1.3) є рівнянням однопорожнинного гіперболоїда, при - рівнянням кругового конуса і при - рівнянням двопорожнинного гіперболоїда.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)