Градієнт, його властивості

Припустимо, що в якійсь точці М одночасно не дорівнюють нулю. В якому напрямку 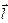похідна має найбільше значення? Відповідь на це запитання має важливе практичне значення.

Означення 3.4. Вектор, координатами якого є значення частинних похідних функції в точці , називається градієнтом функції в цій точці і позначається або чи . Отже,

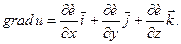(3.15)

Наступна теорема встановлює зв¢язок між похідною функції в даній точці за довільним напрямком та градієнтом функції в цій точці.

Теорема 3.2. Похідна функції 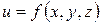в точці за напрямком вектора дорівнює проекції градієнта функції в цій точці на вектор , тобто

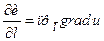. (3.16)

Д о в е д е н н я. Так як 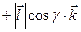, то, згідно властивості проекції та формули для обчислення скалярного добутку векторів через їхні координати, матимемо:

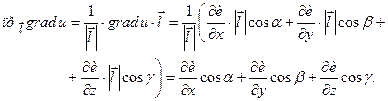
Враховуючи (3.12), отримуємо (3.16), чим і доводимо нашу теорему.

Розглянемо деякі властивості градієнта.

1⁰. Градієнт функції в даній точці вказує напрямок, по якому похідна в цій точці має найбільше значення, яке дорівнює

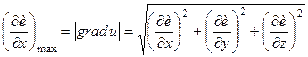. (3.17)

Дійсно, з рівності (3.16) на основі означення проекції маємо

, (3.18)

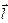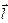де - кут між напрямком вектора та градієнтом функції в даній точці. З (3.18) видно, що у випадку рівність виконуватиметься тоді і тільки тоді, коли , тобто коли вектор співнапрямлений з градієнтом.

Таким чином, скалярне поле в довільній точці зростає найшвидше в напрямку градієнта. Відповідно до (3.13) в напрямку, протилежному до градієнта, воно найшвидше зменшуватиметься.

2⁰. Швидкість зміни скалярного поля в даній точці в напрямку, перпендикулярному градієнту в цій точці, дорівнює нулю.

Справді, якщо 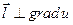, то з рівності (3.16) отримуємо .

3⁰. Градієнт в кожній точці поля перпендикулярний до поверхні рівня, яка проходить через цю точку.

Ця властивість випливає безпосередньо з зауваження 3.2.

4⁰. Нехай - скалярні поля, задані в деякій області. Мають місце наступні рівності:

;

;

;

;

.

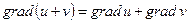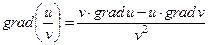Доведення цих рівностей випливає з означення градієнта та правил диференціювання. Доведемо, наприклад, четверту рівність:

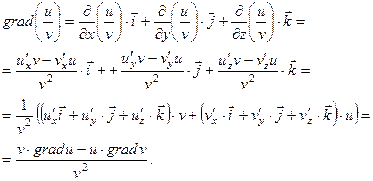
Приклад 3.5. Знайти найбільшу швидкість зростання поля в точці .

Р о з в′ я з а н н я

Знайдемо градієнт поля в заданій точці. Відповідно до (3.15) маємо:

.

Отже, .

Тоді за формулою (3.17) знаходимо

.

Лекція 4 Частинні похідні та диференціали

Поиск по сайту: