Функції

Нехай функція визначена в деякій області D, а аргументи х та у є функціями від t:

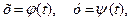(2.18)

визначеними в деякому проміжку 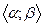, причому для всіх точки .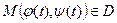

Якщо в функцію замість х та у підставити їх значення з (2.18), то отримаємо складену функцію від одного аргумента t:

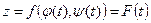. (2.19)

Теорема 2.4. Якщо функції 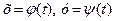в деякій точці 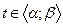мають скінченні похідні, а функція в точці диференційована, то складена функція (2.19) має в точці t похідну, яка дорівнює

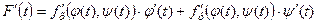. (2.20)

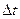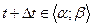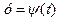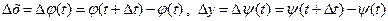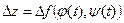Д о в е д е н н я. Надамо аргументу t довільного приросту , такого щоб . Тоді функції , отримають прирости відповідно . Оскільки функція диференційована в точці , то її повний приріст в цій точці можна записати у вигляді (2.7), тобто

Розділивши обидві частини цієї рівності на 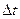, отримаємо:

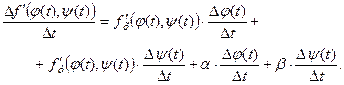(2.21)

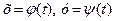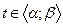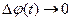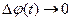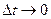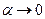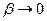Так як функції в точці мають похідні, то вони неперервні в цій точці, тобто та при . Значить, та при 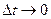. Тому, переходячи до границі в рівності (2.21) при 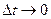, отримуємо рівність (2.20), чим і доводимо нашу теорему.

Зауваження 2.6. Рівність (2.20) можна записати ще й так:

. (2.22)

Зауваження 2.7. Щойно доведену теорему можна узагальнити на випадок, коли аргументи функції є, в свою чергу, функціями декількох змінних, наприклад, двох.

Теорема 2.5. Нехай функція визначена в деякій області D, а аргументи х та у є функціями двох змінних u та v: 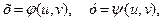які визначені в деякій області G, причому для всіх точок 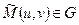відповідні точки .

Тоді якщо функції диференційовані в якійсь точці 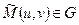, а функція диференційована у відповідній точці 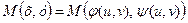, то складена функція 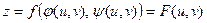має частинні похідні по u та v вточці і ці частинні похідні дорівнюють:

. (2.23)

Доведення цієї теореми аналогічне доведенню попередньої теореми.

Розглянемо приклади.

Приклад 2.5. Знайти похідну 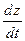функції 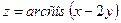, якщо .

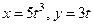Р о з в′ я з а н н я. Скориставшись формулою (2.22), маємо:

Приклад 2.6. Чи задовольняє співвідношенню 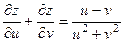функція 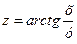, де ?

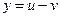Р о з в′ я з а н н я. Використовуючи формули (2.23), знаходимо

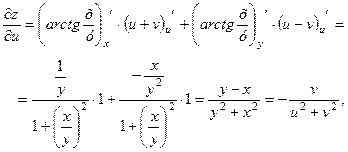
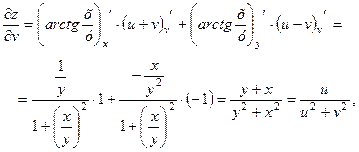
звідки, додавши отримані рівності, переконуємось, що задана функція задовольняє вказаному співвідношенню.

Приклад 2.7 Якщо функція 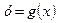має похідну в деякій точці х, а функція диференційована у відповідній точці 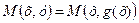, то, міркуючи відповідно до теореми 2.4, матимемо:

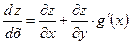(2.24)

Займемось зараз диференціалом складеної функції.

Теорема 2.6. Нехай в деякій точці 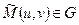функції 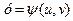мають неперервні частинні похідні 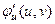, , 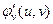, , 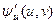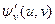а функція має неперервні частинні похідні 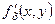та 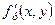у відповідній точці .

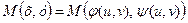Тоді функція , розглядувана як складена функція в точці , має диференціал

.

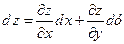Д о в е д е н н я. Відповідно до умов теореми функція 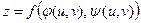має неперервні частинні похідні по u та v в точці . Значить, за теоремою 2.3, вона диференційована в цій точці і її диференціал дорівнює

.

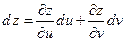Підставивши в цю рівність значення похідних 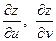з формул (2.23), після перегрупування доданків отримаємо:

.

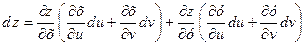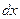Оскільки за умовою теореми функції є неперервними в точці , то вирази в дужках останньої рівності є відповідно диференціали та .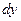

Теорему доведено.

Висновок 2.2. Як бачимо з доведеної теореми, форма повного диференціала зберігається і у випадку складеної функції декількох змінних. Цю властивість називають інваріантністю форми повного диференціала функції декількох змінних.

Поиск по сайту: