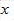Змінних

Нехай функція визначена і неперервна в обмеженій замкнутій області D. Тоді за теоремою 1.2 вона обмежена і досягає своїх найменшого та найбільшого значень, тобто існує хоча б одна точка , в якій значення функції серед усіх інших значень є найменшим і існує хоча б одна точка , в якій значення функції серед усіх інших значень є найбільшим. Ці точки ще називаються відповідно точками глобального мінімуму та глобального максимуму, а значення функції в цих точках – глобальним мінімумом та глобальним максимумом.

Зазначимо, що теорема 1.2 не дає способу знаходження точок 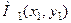та 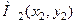, тоді як методи визначення екстремуму функції в окремих випадках дають змогу в деяких випадках знайти її найменше та найбільше значення.

Припустимо, що функція , крім перелічених вище умов, має ще й скінченні частинні похідні першого порядку в усіх внутрішніх точках області D. Якщо точка , в якій функція набуває свого найменшого (найбільшого) значення, знаходиться всередині області D, то вона є точкою екстремуму даної функції, тобто виконуються необхідні умови (5.5) існування екстремуму. Проте функція може набувати свого найменшого (найбільшого) значення в точках, які знаходяться на межі області.

Враховуючи вище сказане, дістаємо наступне правило.

Щоб знайти найменше (найбільше) значення функції ,визначеної і неперервної в обмеженій замкнутій області D, потрібно:

1) знайти всі внутрішні точки області D, в яких функція може мати екстремум, і, якщо цих точок скінченне число, обчислити значення функції в цих точках;

2) знайти, якщо це можна, значення функції, які є найменшим та найбільшим серед усіх значень функції, яких вона набуває на межі даної області;

3) серед усіх обчислених в п. 1) та 2) значень функції вибрати найменше та найбільше числа. Вони і будуть найменшим та найбільшим значеннями функції в області D.

Приклад 5.5. Знайти найменше та найбільше значення функції

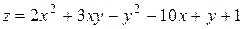(5.18)

в трикутнику, обмеженому прямими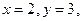

Р о з в′ я з а н н я

Знайдемо спочатку стаціонарні точки даної функції. Координати кожної з таких точок є розв¢язками системи рівнянь виду (5.6). Так як

то система виду (5.6) буде такою:

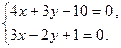
Розв¢язком її буде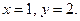

Отже, функція (5.18) має одну стаціонарну точку 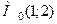, яка знаходиться всередині заданого трикутника (рис. 5.1). Обчислюємо значення функції в цій точці:

.

Тепер досліджуємо нашу функцію на межі області, тобто на сторонах трикутника АВС.

І. Візьмемо сторону АВ. В цьому випадку 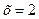, , 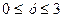тому задана функція (5.18) вироджується в функцію однієї змінної у, задану на відрізку :

Знаходимо точки, в яких функція 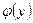може приймати найменше та найбільше значення і обчислюємо значення 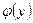в цих точках.

,

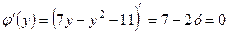звідки 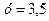. Ця точка не належить відрізку , тому обчислюємо значення функції 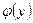тільки на кінцях відрізка :

,

.

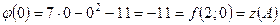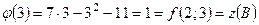ІI. На стороні ВС маємо 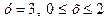, отже функція (5.18) набуває вигляду

.

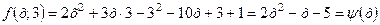Тепер аналогічно до попереднього поступаємо з функцією 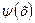на відрізку .

,

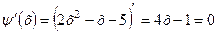звідки 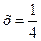. Ця точка знаходиться всередині відрізка . Тому обчислюємо

,

а також

.

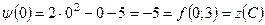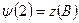уже обчислено вище.

ІII. На стороні АС 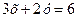, звідки 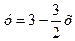. Значить, функція (5.18) виглядатиме так:

.

де х змінюється на відрізку . Оскільки на кінцях цього відрізка вище уже обчислено 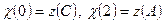, то нам залишилось обчислити стаціонарні точки функції на відрізку та обчислити її значення в цих точках.

,

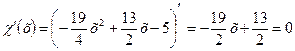звідки 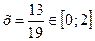, тому обчислюємо

.

Тепер серед усіх обчислених значень функції (5.18) вибираємо найменше та найбільше. Вони і будуть шуканими її найменшим та найбільшим значеннями в заданій області.

Отже,

, .

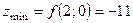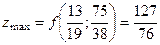Зауваження 5.3. Ми детально вивчили екстремум на прикладі функції двох змінних. Відзначимо, що значна частина міркувань залишається справедливою і для функцій більше ніж двох змінних. Зокрема, правило знаходження найменшого (найбільшого) значення функції залишається таким самим, як і для функції двох змінних. Проте достатні умови існування екстремуму функції п > 2 змінних значно складніші, ніж достатні умови для функції двох змінних.

Поиск по сайту: