 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Диференціювання неявних функцій
Ми звикли вивчати функції однієї чи багатьох змінних, які задавались рівняннями, розв¢язаними відносно цієї функції, тобто рівнянням
 ,
,
якщо йшлося про функцію однієї змінної, чи рівнянням (1.1) або (1.2) для функції двох або трьох змінних.
Відзначимо, що часто функцію задають рівнянням, не розв¢язаним відносно цієї функції,
 . (2.25)
. (2.25)
Розглянемо, наприклад, рівняння
 . (2.26)
. (2.26)
Так як кожному значенню 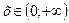 дане рівняння ставить у відповідність два різних значення
дане рівняння ставить у відповідність два різних значення  , то воно при значеннях
, то воно при значеннях 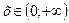 не задає у як функціювід х. Але, якщо х та у брати з певного околу точки
не задає у як функціювід х. Але, якщо х та у брати з певного околу точки  , яка лежить на параболі (рис. 2.1) і не збігається з її вершиною – точкою О, то в цьому околі рівняння (2.26) задає у як функцію від х. Разом з тим, в будь-якому околі точки О рівняння (2.26) не визначає у як функцію від х.
, яка лежить на параболі (рис. 2.1) і не збігається з її вершиною – точкою О, то в цьому околі рівняння (2.26) задає у як функцію від х. Разом з тим, в будь-якому околі точки О рівняння (2.26) не визначає у як функцію від х.
 З розглянутого приклада випливає, що рівняння виду (2.26) може задавати у як функцію від х в околі однієї точки, координати якої задовольняють це рівняння, а в околі іншої точки рівняння (2.26) не задає у як функцію від х.
З розглянутого приклада випливає, що рівняння виду (2.26) може задавати у як функцію від х в околі однієї точки, координати якої задовольняють це рівняння, а в околі іншої точки рівняння (2.26) не задає у як функцію від х.
Природньо поставити наступне запитання: яким умовам повинна задовольняти функція  , щоб рівняння (2.25) в деякому околі точки, координати якої задовольняють цьому рівнянню, визначало у як функцію від х і щоб ця функція була неперервною та диференційованою?
, щоб рівняння (2.25) в деякому околі точки, координати якої задовольняють цьому рівнянню, визначало у як функцію від х і щоб ця функція була неперервною та диференційованою?
Дамо наступне
Означення 2.3. Нехай області визначення функції  належить прямокутник
належить прямокутник  . Якщо для кожного
. Якщо для кожного  рівняння (2.25) має один і тільки один корінь
рівняння (2.25) має один і тільки один корінь  з відрізка
з відрізка  , то
, то  називається неявною функцією від х, заданою рівнянням (2.25).
називається неявною функцією від х, заданою рівнянням (2.25).
Таким чином, якщо функція  , задана рівнянням (2.25), є неявною, то для всіх
, задана рівнянням (2.25), є неявною, то для всіх  виконується тотожність
виконується тотожність
 . (2.27)
. (2.27)
Теорема 2.7. Нехай функція  визначена, неперервна та має неперервні частинні похідні в деякому околі точки
визначена, неперервна та має неперервні частинні похідні в деякому околі точки  , причому
, причому  ,
,  .
.
Тоді існує такий окіл точки  , в якому рівняння (2.25) визначає єдину неявну функцію
, в якому рівняння (2.25) визначає єдину неявну функцію  , неперервну та диференційовану в околі точки
, неперервну та диференційовану в околі точки  , і таку що
, і таку що  .
.
Доведення цієї теореми опускаємо. Його можна знайти, наприклад, в [1].
Знайдемо похідну неявної функції. Відповідно до умов теореми, на деякому інтервалі, якому належить точка х 0, виконується тотожність (2.27). так як похідна функції, що тотожно дорівнює нулю, також дорівнює нулю, то повна похідна  . Але, використовуючи рівність (2.24), маємо
. Але, використовуючи рівність (2.24), маємо  , тому
, тому  . Зокрема, в точці
. Зокрема, в точці  матимемо
матимемо  , звідки, оскільки
, звідки, оскільки  , отримуємо
, отримуємо
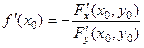 . (2.28)
. (2.28)
Приклад 2.8. Знайти похідну  функції, заданої рівнянням
функції, заданої рівнянням  .
.
Р о з в′ я з а н н я. В нашому випадку
 ,
,  ,
,
 .
.
Значить, відповідно до формули (2.28), матимемо
 .
.
Зауваження 2.8. Інколи буває, що функція  задовольняє всім умовам теореми 2.7, тільки
задовольняє всім умовам теореми 2.7, тільки  , але
, але  . Тоді рівняння (2.25) задає х як неявну функцію від у:
. Тоді рівняння (2.25) задає х як неявну функцію від у:  . Ця функція має ті ж властивості, що й функція
. Ця функція має ті ж властивості, що й функція  , зокрема,
, зокрема,  має неперервну частинну похідну
має неперервну частинну похідну
 .
.
Ми розглянули питання про неявну функцію однієї змінної. Аналогічно можна розглянути неявну функцію багатьох змінних. Зупинимось, наприклад, на неявній функції двох змінних.
Розглянемо рівняння
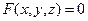 (2.29)
(2.29)
Означення 2.4. Нехай області визначення функції  належить паралелепіпед
належить паралелепіпед 
 . Якщо для кожної точки
. Якщо для кожної точки  з прямокутника
з прямокутника  рівняння (2.25) має один і тільки один корінь
рівняння (2.25) має один і тільки один корінь  з відрізка
з відрізка  , то
, то  називається неявною функцією від двох змінних х та у, заданою рівнянням (2.29).
називається неявною функцією від двох змінних х та у, заданою рівнянням (2.29).
Отже, якщо функція  , задана рівнянням (2.29), є неявною, то для всіх точок
, задана рівнянням (2.29), є неявною, то для всіх точок  з прямокутника
з прямокутника  виконується тотожність
виконується тотожність
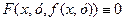 .
.
Аналогічно до теореми 2.7 має місце наступна
Теорема 2.8. Нехай функція  визначена, неперервна та має неперервні частинні похідні в деякому околі точки
визначена, неперервна та має неперервні частинні похідні в деякому околі точки 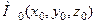 , причому
, причому  ,
,  .
.
Тоді існує такий окіл точки 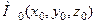 , в якому рівняння (2.29) визначає єдину неявну функцію
, в якому рівняння (2.29) визначає єдину неявну функцію  , неперервну та диференційовану в околі точки
, неперервну та диференційовану в околі точки  , і таку що
, і таку що  .
.
Доведення цієї теореми також опускаємо. Відзначимо, що воно аналогічне доведенню теореми 2.7.
Знайдемо частинні похідні неявної функції z від х та у, заданої рівнянням (229). Коли визначаємо  (або
(або  ), то змінну у (або х) вважаємо сталою, тому, використовуючи (2.28), отримуємо:
), то змінну у (або х) вважаємо сталою, тому, використовуючи (2.28), отримуємо:
 (2.30)
(2.30)
Приклад 2.8. Знайти повний диференціал функції  , якщо
, якщо
 . (2.31)
. (2.31)
Р о з в′ я з а н н я. Очевидно, рівність (2.31) можна переписати так: 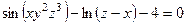 . Тому в нашому випадку маємо
. Тому в нашому випадку маємо
 ,
,  ,
,  ,
,
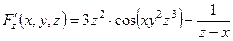 .
.
Значить, відповідно до формул (2.30), знаходимо
 ,
,
 ,
,
звідки, використовуючи (2.11), отримуємо
 .
.
Зауваження 2.9. Якщо умова  не виконується, зате, наприклад,
не виконується, зате, наприклад,  і виконуються всі інші умови теореми 2.8, то рівняння (2.29) в околі точки
і виконуються всі інші умови теореми 2.8, то рівняння (2.29) в околі точки 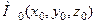 задає х як функцію двох змінних
задає х як функцію двох змінних  . При цьому
. При цьому  ,
,  .
.
Лекція 3 Деякі застосування частинних
Поиск по сайту: