Умовний екстремум

В попередніх пунктах цієї лекції ми розглянули екстремум функції, коли на незалежні змінні не накладалося ніяких додаткових умов. Але на практиці часто зустрічаються такі екстремальні задачі, коли на незалежні змінні накладаються ще додаткові умови.

Наприклад, для функції треба знайти екстремум не в усій її області існування , а тільки в точках деякої кривої із цієї області

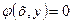. (5.19)

Такий екстремум називають умовним (розглянутий вище екстремум називають безумовним). Зауважимо, що якщо рівняння (5.19) допускає розв¢язання відносно однієї зі змінних, то, підставивши це значення у функцію , матимемо безумовний екстремум для функції однієї змінної. Проте далеко не завжди це легко зробити.

Ми розглянемо метод дослідження функції на умовний екстремум, який не вимагає розв¢язання рівнянь типу (5.19) чи системи таких рівнянь відносно деяких змінних – метод невизначених множників Лагранжа.

Не зменшуючи загальності, з¢ясуємо суть цього метода на прикладі функції двох змінних.

Отже, нехай функція

(5.20)

задана в деякій області , а на незалежні змінні х та у накладено умову (5.19).Зазначимо, що умов повинно бути менше, ніж незалежних змінних.

Рівняння (5.19) називається рівнянням зв¢язку.

Означення 5.2. Точка , координати якої задовольняють рівнянням зв¢язку (5.21), називається точкою умовного мінімуму (максимуму) функції , якщо існує окіл цієї точки , такий що для всіх точок 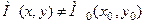із цього околу, координати яких задовольняють рівнянню зв¢язку (5.19), виконується нерівність

Число називається умовним мінімумом (максимумом). Точка умовного мінімуму (максимуму) називається точкою умового екстремуму, а число - умовним екстремумом.

Виведемо необхідні умови того, щоб точка була точкою умовного мінімуму (максимуму) функції .

Припустимо, що точка є точкою умовного екстремуму і, крім того, виконуються умови:

1) функція в має неперервні частинні похідні першого порядку;

2) функція в задовольняє умовам теореми 2.7 про існування неявної функції, заданої рівнянням (5.19).

Отже, згідно з припущенням 2), рівняння (5.19) задає в функцію 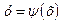, яка в точці має похідну (п. 2.4)

. (5.21)

Крім того, якщо значення 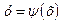підставити в (5.20), то задача про умовний екстремум в точці зводиться до задачі про безумовний екстремум для складеної функції однієї змінної

. (5.22)

У цьому випадку похідна першого порядку від функції (5.22) в точці дорівнює нулю. За правилами диференціювання складеної функції (див. (2.24)) маємо

.

Поклавши в останній рівності 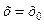, з врахуванням (5.21) отримаємо

,

звідки

.

Позначивши останні відношення через 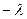(знак мінус взято для зручності, а саме число може мати довільний знак), маємо

,

тобто

.

Враховуючи ще й (5.20), бачимо, що координати точок умовного екстремуму повинні задовольняти систему рівнянь

(5.23)

Аналізуючи цю систему, помічаємо, що її рівняння є необхідними умовами екстремуму функції

. (5.24)

Функція (5.24) називається функцією Лагранжа, а число - множником Лагранжа.

Як уже сказано, умови (5.23) є лише необхідними. Вони дають змогу знайти стаціонарні точки умовного екстремуму. Враховуючи формулу Тейлора у вигляді (4.21), характер умовного екстремуму (достатні умови) можна встановити за знаком диференціала другого порядку функції Лагранжа в стаціонарній точці

причому dx та dу зв¢язані співвідношенням

. (5.25)

А саме, якщо , то точка є точкою умовного мінімуму (максимуму)

Приклад 5.6. Знайти екстремуми функції при умові .

Р о з в′ я з а н н я

Очевидно, рівняння зв¢язку буде таким:

.

Отже, функція Лагранжа (5.24) матиме вигляд

.

Так як

.

то система рівнянь (5.23) виглядатиме так:

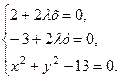
Розв¢язуючи цю систему, знаходимо два розв¢язки: Таким чином, точками умовного екстремуму можуть бути точки та 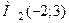. Перевіримо, чи це так, знайшовши для кожної з точок .

Оскільки

то

.

Значить, для точки матимемо

,

тому є точкою умовного максимуму, а для точки матимемо

,

тому є точкою умовного мінімуму для заданої функції. При цьому

, .

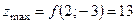Зауваження 5.4. В щойно розглянутому прикладі не було потреби знаходити співвідношення (5.25) між dx та dу, так як ми і без цього чітко встановили знак для кожної з точок та .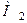

Зауваження 5.5. Розглянутий метод невизначених множників Лагранжа можна поширити на дослідження функції довільного числа змінних на умовний екстремум. Зокрема, для функції трьох змінних з рівняннями зв¢язку 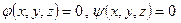фунція Лагранжа буде такою:

.

Тому стаціонарні точки умовного екстремуму потрібно знаходити із системи п¢яти рівнянь з п¢ятьма невідомими

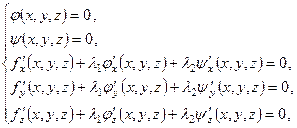
а достатні умови існування умовного екстремуму в цих точках можна визначити за знаком диференціала .

Поиск по сайту: