Диференціали вищих порядків

Нехай функція визначена і має неперервні частинні похідні в області . Тоді за теоремою 2.3 вона диференційована в кожній точці , отже, має повний диференціал

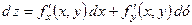(4.10)

Цей диференціал називатимемо диференціалом першого порядку. Як бачимо, диференціал першого порядку 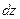є функцією від х та у; , - прирости незалежних змінних, і вони розглядаються як сталі числа. Якщо функція 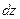, або частинні похідні мають, в свою чергу, неперервні частинні похідні першого порядку, то можемо стверджувати, що 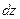має диференціал .

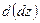Означення 4.2. Диференціал першого порядку від диференціала першого порядку називається диференціалом другого порядку функції в точці і позначається символом 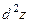, тобто

(4.11)

Використовуючи це означення, виведемо формулу для диференціала другого порядку. Підставляючи значення 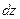з (4.10) в (4.11), дістаємо

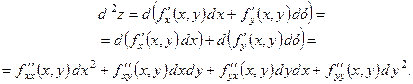Ми позначили . За припущенням мішані частинні похідні неперервні в точці , тому за теоремою 4.1 вони рівні між собою, тобто

.

Таким чином, для диференціала другого порядку маємо таку формулу:

(4.12)

Очевидно, диференціал другого порядку є функцією від х та у, тому він може мати диференціал першого порядку.

Відповідно до означення 4.2 диференціал першого порядку від диференціала другого порядку називається диференціалом третього порядку функції в точці і позначається символом , тобто

. (4.13)

Якщо функція має неперервні частинні похідні третього порядку в області D, то 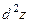є диференційованою функцією, отже, має диференціал. Підставивши (4.12) в (4.13), дістанемо формулу для диференціала третього порядку:

(4.14)

Індуктивно можна означити диференціали четвертого, п¢ятого і т.д., п –го порядків: якщо маємо диференціал (п - 1) –го порядку функції , то диференціал першого порядку від цього диференціала називають диференціалом п –го порядку функції , тобто .

Відзначимо, що коли для позначення частинних похідних користуватися символами , , , і т.д., то формули (4.10), (4.12) та (4.14) можна записати компактніше:

,

,

.

Для диференціала п –го порядку матимемо

. (4.15)

Формулу (4.15) називають символічно степеневою формулою. В розгорнутому вигляді вона запишеться так:

де - число комбінацій з п по k:

.

Зауваження 4.3. Враховуючи зауваження 2.3, ми можемо, аналогічно до (4.15), записати диференціал п –го порядку у випадку його існування функції трьох і більшої кількості змінних. Зокрема, для функції трьох змінних 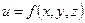матимемо:

. (4.16)

Розглянемо приклади.

Приклад 4.3. Знайти 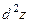функції в точці .

Р о з в′ я з а н н я

Ми скористаємось формулою (4.12). Для цього знайдемо частинні похідні першого та другого порядків:

, ,

,

, .

Тоді

,

звідки .

Приклад 4.4. Знайти функції в довільній точці .

Р о з в′ я з а н н я

Знайдемо усі частинні похідні до третього порядку включно:

, , ,

, ,

, ,

,

.

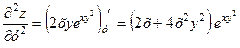Скориставшись формулою (4.14) та винісши за дужки, матимемо:

Приклад 4.5. Знайти 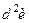функції .

Р о з в′ я з а н н я

Для заданої функції трьох змінних знаходимо спочатку усі частинні похідні до другого порядку включно:

,

, ,

, ,

, ,

, .

Тепер скористаємось формулою (4.16), яка в розгорнутому виді при п = 2 буде такою:

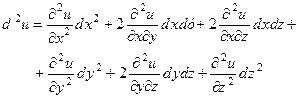
Підставивши в цю формулу знайдені частинні похідні, дістанемо

.

Зауваження 4.4. Відзначимо, що на відміну від диференціала першого порядку диференціали вищих порядків не мають властивості інваріантності. Переконаємось в цьому на прикладі диференціала другого порядку.

Нехай функція визначена в деякій відкритій області D, а - функції, визначені на проміжку 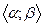, причому для всіх 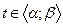точки .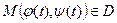

Припустимо, що функція 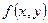має неперервні частинні похідні в області D до другого порядку включно, а функції мають неперервні похідні на проміжку 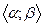до другого порядку включно. Значить, функція 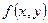має диференціали першого та другого порядків. Отже,

.

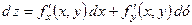Тут 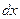та 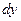на відміну від розглянутого вище випадку не є сталими величинами, а функціями від t:

.

Тоді, відповідно до означення диференціала другого порядку, матимемо

Розкриваючи диференціали, отримуємо

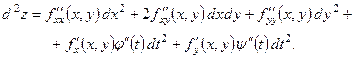
Як бачимо, на відміну від формули (4.12), тут з¢явились нові доданки:

Очевидно, ці доданки не завжди рівні нулю. Отже, форма диференціала другого порядку не зберігається.

Поиск по сайту: