Означення функції декількох змінних

В природі та в техніці досить часто зустрічаються випадки, коли явища й процеси описуються двома та більше величинами. В цьому можна переконатись наступними простими прикладами.

Приклад 1.1. Площа бічної поверхні 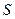кругового конуса з радіусом основи 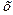та твірною визначається формулою

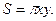
Як бачимо, кожній парі значень 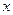та відповідає певне значення площі .

Приклад 1.2. Об’єм 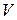прямокутного паралелепіпеда з ребрами 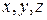обчислюється за формулою

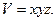
В даному випадку кожній впорядкованій трійці значень 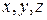відповідає певне значення об¢єма .

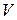Означення 1.1. Якщо кожній точці 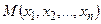із деякої області D, яка є підмножиною евклідового простору 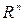, поставлено у відповідність одне єдине дійсне число 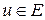(E – деяка підмножина множини дійсних чисел), то кажуть, що на множині Е задано функцію п змінних і записують

, або ;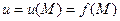

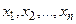називають незалежними змінними або аргументами, множину D – областю визначення або областю існування функції, а множину Е – множиною значень функції.

Зауваження 1.1. Інколи зустрічаються випадки, коли точці ставиться у відповідність декілька дійсних чисел 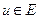. В такому випадку говорять про багатозначні функції декількох змінних. Надалі ми ці випадки не розглядатимемо.

Зауваження 1.2. Надалі, оскільки не виникатиме порушення загальності міркувань, розглядатимемо функції двох або трьох змінних. Це дасть змогу спростити запис і виклад теорії. Для зручності функцію двох змінних записуватимемо у вигляді

, (1.1)

а функцію трьох змінних - у вигляді

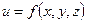. (1.2)

Зауваження 1.3. Як правило, під областю визначення функції розумітимемо так звану природню область визначення функції – множину всіх точок 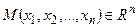, для яких вираз має зміст.

Приклад 1.3. Знайти область визначення функції .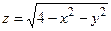

Оскільки підкореневий вираз не може бути від’ємним, то областю визначення буде множина всіх точок М (х, у)площини, для яких 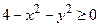або 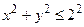, тобто замкнутий круг з центром в початку координат і радіусом 2 (рис. 1.1).

Означення 1.2. Для функції двох змінних 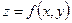, визначеної в області D, геометричне місце точок для всіх 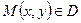називатимемо графіком цієї функції.

Виходячи з цього означення, ми бачимо, що графіком функції двох змінних буде деяка поверхня в просторі. Наприклад, для розглянутої 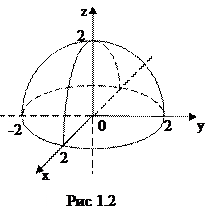вище функції 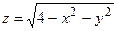її графіком буде верхня півсфера з центром в початку координат і радіусом R= 2 (рис. 1.2).

Відзначимо, що в загальному випадку не вдається побудувати графік функції двох змінних та визначити його вигляд. Також слід зауважити, що функцію трьох і більше змінних геометрично зобразити вже не можна, оскільки наш простір тривимірний.

Поиск по сайту: