Неперервність функції декількох змінних

Нехай функція двох змінних визначена в деякій області D. Точка і є внутрішньою або межовою для D.

Означення 1.7. Функція називається неперервною в точці , якщо

, (1.7)

причому точка прямує до точки довільним чином, залишаючись в області визначення функції.

Якщо функція неперервна в кожній точці деякої області, то вона називається неперервною в цій області.

Якщо функція не є неперервною в точці, то вона називається розривною в цій точці, а сама точка називається точкою розриву даної функції.

Використовуючи означення неперервності функції декількох змінних та відповідні теореми про границі, можна довести, що арифметичні операції над неперервними функціями та побудова складеної функції з неперервних функцій приводять до неперервних функцій.

Функцію декількох змінних називатимемо елементарною, якщо вона є елементарною по кожному зі своїх аргументів.

Сформулюємо без доведення наступну важливу теорему.

Теорема 1.1. Кожна елементарна функція декількох змінних є неперервною в усіх точках своєї області визначення.

Приклад 1.9. Дослідимо на неперервність розглянуту в прикладі 1.8 функцію.

В усіх точках площини, відмінних від початку координат, , тобто є елементарною, а значить, і неперервною. Ми показали, що в точці О(0;0) наша функція не має границі, отже вона не може бути неперервною в цій точці, тобто є розривною.

Разом з тим, та , тому та 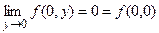, тобто що в точці О(0;0) задана функція неперервна по кожному зі своїх аргументів.

Отже, на основі щойно розглянутого приклада можемо зробити висновок, що з неперервності функції декількох змінних по кожному зі своїх аргументів в деякій точці ще не випливає неперервність її в цій точці, хоча навпаки, звичайно, вірно.

Для формулювання подальших властивостей неперервних функцій нам потрібні будуть наступні означення.

Означення 1.8. Область називається відкритою, якщо всі її точки внутрішні.

Означення 1.9. Область називається замкнутою, якщо цій області належать всі її межові точки. Множина всіх межових точок області називається її межею.

Означення 1.10. Область на площині (в просторі) називається обмеженою, якщо вона повністю міститься в деякому крузі (деякій кулі).

Означення 1.11. Область називається зв’язною, якщо дві її довільні точки можна з’єднати неперервною лінією, яка повністю належить цій області.

Теорема 1.2. Нехай функція декількох змінних визначена і неперервна в деякій обмеженій замкнутій області D. Тоді мають місце наступні властивості.

1 ⁰. - обмежена в D, тобто існує таке число , що для всіх виконується нерівність .

2 ⁰. Дана функція досягає в D своїх найменшого та найбільшого значень, тобто існують такі точки та , що для всіх виконується нерівність .

3 ⁰. Якщо область D є щей зв’язною, то приймає всі проміжні значення між своїми найменшим та найбільшим, тобто для довільного існує така точка , що .

Поиск по сайту: