Декількох змінних

Нехай функція визначена в деякій відкритій області D. Візьмемо в цій області довільну точку . Якщо зафіксувати , то розглядувана функція є функцією однієї змінної, а саме функцією від .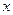

Надамо х довільного приросту так, щоб точка належала області D. Тоді функція отримає приріст , який називається частинним приростом функції по х в точці і позначають

, (1.8)

або .

Аналогічно позначають частинний приріст по у в точці :

. (1.9)

Візьмемо ще якусь точку в області D, відмінну від . Різниця значень функції в точках М та називається повним приростом функції і визначається формулою

. (1.10)

Слід відзначити, що, взагалі кажучи, повний приріст не дорівнює сумі частинних приростів.

Аналогічним чином визначаються частинні та повний прирости функцій довільної кількості змінних. Наприклад, для функції трьох змінних 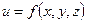матимемо:

,

,

,

.

Повернемось до означення неперервності функції. Якщо позначити , , то рівність (1.7) можна переписати так:

або

. (1.11)

Рівність (1.11) дає ще одне означення неперервності.

Аналогічно до (1.11) отримуємо, що функція неперервна: по аргументу х в точці , якщо ;по аргументу у в точці , якщо .

Поиск по сайту: