 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Диференціал функції декількох змінних
Нехай функція  диференційована в точці
диференційована в точці  . Тоді її повний приріст в цій точці можна записати у вигляді (2.7)
. Тоді її повний приріст в цій точці можна записати у вигляді (2.7)
Означення 2.2. Вираз
 (2.8)
(2.8)
називається повним диференціалом функції  в точці
в точці  .
.
Відзначимо, що, крім записаного позначення 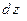 часто повний диференціал позначають
часто повний диференціал позначають  .
.
Якщо  - довільна точка області D, в якій функція диференційована, то повний диференціал в цій точці записуватимемо
- довільна точка області D, в якій функція диференційована, то повний диференціал в цій точці записуватимемо
 . (2.9)
. (2.9)
Зауваження 2.4. Якщо покласти за означенням  ,
,  , то повний диференціал в довільній точці
, то повний диференціал в довільній точці  запишеться у вигляді
запишеться у вигляді
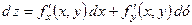 (2.10)
(2.10)
або
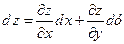 . (2.11)
. (2.11)
Розглянемо приклади.
Приклад 2.2. Знайти повний диференціал функції  в точці
в точці  .
.
Р о з в′ я з а н н я
В прикладі 1.10 а) ми знайшли частинні похідні заданої функції. Значення їх в заданій точці дорівнюватимуть:
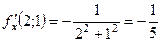 ,
,  .
.
Тоді, відповідно до (2.10), шуканий диференціал в заданій точці буде таким:
 .
.
Зауваження 2.5. Як бачимо з (2.11), повний диференціал функції двох змінних дорівнює сумі добутків частинних похідних по кожному з аргументів на диференціали цих аргументів. Так само визначається повний диференціал функції більшої кількості аргументів. Зокрема, повний диференціал для функції трьох змінних 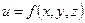 у випадку її диференційованості виглядатиме так:
у випадку її диференційованості виглядатиме так:
 . (2.12)
. (2.12)
Приклад 2.3. Знайти повний диференціал функції  .
.
Р о з в′ я з а н н я
Підставивши знайдені в прикладі 1.10 б) частинні похідні для заданої функції в (2.12), отримаємо
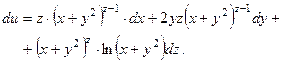
Займемось оцінкою двох останніх доданків правої частини рівності (2.7).
Розглянемо величину  . Зрозуміло, що
. Зрозуміло, що  тоді і тільки тоді, коли одночасно
тоді і тільки тоді, коли одночасно  та
та  .
.
Суму двох останніх доданків правої частини (2.7) можна записати в такому вигляді:
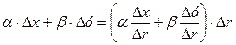 . (2.13)
. (2.13)
Позначимо
 . (2.14)
. (2.14)
Оскільки 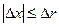 ,
,  , а на основі рівностей (2.2)
, а на основі рівностей (2.2) 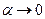 та
та 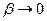 при
при  , то й
, то й
 при
при  . (2.15)
. (2.15)
З врахуванням (2.8), (2.13) та (2.14) рівність (2.7) можемо переписати так:
 . (2.16)
. (2.16)
Тоді  .
.
Висновок 2.1. Отже, у випадку диференційованості функції в деякій точці різниця між її повним приростом та повним диференціалом в цій точці є нескінченно малою вищого порядку, ніж  , при
, при  . Тому повний диференціал функції dz ще називають головною частиною приросту функції.
. Тому повний диференціал функції dz ще називають головною частиною приросту функції.
Відповідно до зробленого висновку можемо записати
 ,
,
або
 . (2.17)
. (2.17)
Цю формулу використовують для наближеного обчислення значення функції в незручній для обчислення точці  через значення функції та її частинних похідних в зручнішій для обчислення точці
через значення функції та її частинних похідних в зручнішій для обчислення точці  . Зрозуміло, що чим точка М 0 ближча до точки М, тим наближена рівність (2.17) точніша.
. Зрозуміло, що чим точка М 0 ближча до точки М, тим наближена рівність (2.17) точніша.
Приклад 2.4. Обчислити наближено  .
.
Р о з в′ я з а н н я
Розглянемо функцію двох змінних  .
.
Очевидно, нам потрібно знайти значення цієї функції в точці М (2,04; 0,97). В точці М 0(2; 1) значення функції обчислюється легко:
 .
.
Отже, візьмемо: 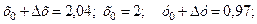
 .
.
Тоді  .
.
Знайдемо частинні похідні розглядуваної функції:
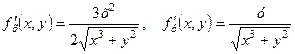 .
.
Значення цих частинних похідних в точці М 0(2; 1) дорівнюватимуть:
 .
.
Підставивши обчислені значення в (2.17), знаходимо
 .
.
Поиск по сайту: