Двох змінних

Нехай маємо деяку поверхню , задану рівнянням

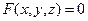. (3.1)

Точка 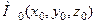належить цій поверхні і входить в область визначення функції разом зі своїм якимось околом, а сама функція диференційована в точці 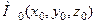, причому не всі частинні похідні в цій точці дорівнюють нулю, тобто

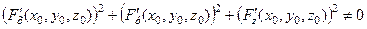. (3.2)

Розглянемо довільну криву L, яка проходить через точку М ₀, має дотичну в цій точці, лежить на поверхні (3.1) і задається рівняннями

,

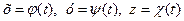причому точці М ₀ відповідає значення параметра t ₀.

Оскільки крива L лежить на поверхні, то координати її точок задовольняють рівнянню (3.1):

. (3.3)

На основі вищесказаного виконуються всі умови теореми по диференціювання складеної функції в точці t ₀.

Тому, продиференціювавши рівність (3.3), отримуємо

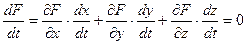. (3.4)

Ця рівність означає перпендикулярність векторів та 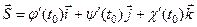, причому другий з них є напрямним вектором дотичної до кривої L в точці М ₀.

Висновок 3.1. З рівності (3.4) випливає, що дотичні до всіх кривих, які лежать на поверхні (3.1) і проходять через точку М ₀, перпендикулярні до одного й того самого вектора 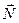. Значить, усі ці дотичні лежать в одній і тій самій площині, яка називається дотичною площиною до поверхні в точці М ₀.

Запишемо рівняння дотичної площини як рівняння площини, що проходить через точку М ₀ перпендикулярно до вектора :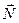

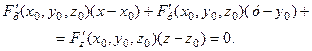. (3.5)

Означення 3.1. Нормаллю до поверхні в точці М ₀ називається пряма, що проходить через точку М ₀ перпендикулярно до дотичної площини в цій точці.

Відповідно до цього означення запишемо рівняння нормалі як канонічні рівняння прямої, що проходить через точку М ₀ і має напрямний вектор :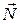

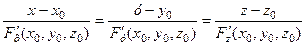. (3.6)

Зауваження 3.1. Ми розглянули випадок, коли функція (3.1) диференційована в точці М ₀ і виконується (3.2). Якщо ці умови не виконуються в деякій точці (її називають особливою), то дотична площина та нормаль в такій точці можуть і не існувати.

Зауваження 3.2. Якщо для деякої функції 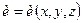рівняння (3.1) є поверхнею рівня, тобто 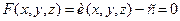, то вектор

буде напрямним вектором нормалі до цієї поверхні

Зауваження 3.3. Якщо рівняння поверхні задано в явній формі , то, взявши , маємо

, , .

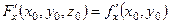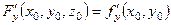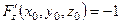Тоді рівняння (3.5) та (3.6) наберуть відповідно такого вигляду:

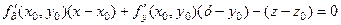; (3.7)

. (3.8)

Розглянемо приклади.

Приклад 3.1. Записати рівняння дотичної площини та нормалі до гіперболоїда 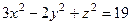в точці .

Р о з в′ я з а н н я

В нашому випадку маємо 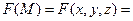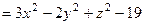, , 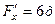, 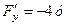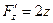. Тому , , .

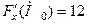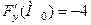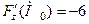Значить, скориставшись рівняннями (3.5) та (3.6), шукані рівняння дотичної площини та нормалі матимуть вигляд:

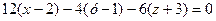
або

;

або

.

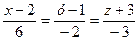Приклад 3.2. Записати рівняння дотичної площини та нормалі до параболоїда в точці .

Р о з в′ я з а н н я

В даному випадку , ,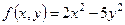

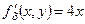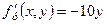. Отже, , .

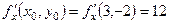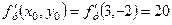Тому, підставивши обчислені значення в формули (3.7) та (3.8), після спрощень матимемо:

- рівняння дотичної площини;

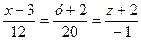- рівняння нормалі.

З¢ясуємо тепер геометричний зміст повного диференціала функції , диференційованої в точці . Поклавши , , 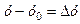рівність (3.7) можемо переписати так:

.

Права частина останньої рівності є повним диференціалом функції в точці , отже .

Таким чином, повний диференціал функції двох змінних у точці дорівнює приросту аплікати точки на дотичній площині до поверхні в точці , якщо від точки перейти до точки (рис. 3.1). В цьому полягає геометричний зміст повногодиференціала функції двох змінних.

Поиск по сайту: